Mapping a 2D Array to a 1D Array: A Comprehensive Exploration

In computer science, we often encounter the need to store two-dimensional (2D) arrays in memory. From a user’s perspective, 2D arrays provide an intuitive way to represent matrix-like data structures or tables, similar to a relational database. However, computers allocate memory linearly, making it essential to convert 2D arrays into one-dimensional (1D) representations for efficient storage.

Understanding this mapping is fundamental for programming tasks, particularly in low-level languages like C and Assembly, where we manage memory directly. Let’s dive into the process of mapping 2D arrays to 1D arrays, the techniques involved, and the formulas used for addressing elements in memory.

Why Map a 2D Array to a 1D Array?

2D arrays allow developers to work with rows and columns, making it easy to handle data that logically fits a grid structure. For instance, a 3 x 3 array can represent a 3×3 matrix in mathematics, a chessboard, or even pixel data in an image matrix.

However, in the computer’s memory, we must store this grid as a linear sequence of elements. This is achieved by mapping the 2D array elements into a 1D structure, which preserves the array’s logical structure while making efficient use of memory.

Understanding the Size of a 2D Array

The size of a 2D array, a[m][n], where m is the number of rows and n is the number of columns, is determined by multiplying m and n. For instance, a 3 x 3 array requires storage for 3 * 3 = 9 elements. This rule helps in memory allocation and in determining the size of the 1D array used to map the 2D array.

Techniques for Storing 2D Array Elements in Memory

There are two common techniques for storing 2D arrays in memory:

• Row Major Order
• Column Major Order

Let’s explore each in detail.

Row Major Order

In row-major order, elements of each row of the 2D array are stored contiguously in memory, meaning we store one complete row, and then move to the next row. This technique is common in C programming, which follows row-major storage for multi-dimensional arrays.

Consider the following 3 x 3 matrix:

a[3][3] = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

Using row-major order, the array would be stored as follows:

[1, 2, 3, 4, 5, 6, 7, 8, 9]

Each row is stored in sequence. The memory address of any element a[i][j] in a 2D array stored in row-major order is calculated as:

Address(a[i][j]) = Base Address + (i * n + j) * Element Size

Where:

• Base Address (BA) is the memory address of the first element a[0][0].
• i is the row index, j is the column index.
• n is the number of columns in the array.
• Element Size is the amount of memory required to store a single element (e.g., 4 bytes for an integer).

Example Calculation:
If a[3][3] starts at the base address 1000 with Element Size 4 bytes, the address of a[1][2] would be:

Address(a[1][2]) = 1000 + (1 * 3 + 2) * 4 = 1000 + (5 * 4) = 1000 + 20 = 1020

Thus, a[1][2] is stored at memory address 1020.

Column Major Order

In column-major order, elements of each column of the 2D array are stored contiguously in memory. This ordering is common in languages like Fortran and MATLAB, which prefer column-major storage for matrices.

Using the same 3 x 3 matrix example:

a[3][3] = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

In column-major order, the array is stored as follows:

[1, 4, 7, 2, 5, 8, 3, 6, 9]

Each column is stored in sequence. The memory address of any element a[i][j] in a 2D array stored in column-major order is calculated as:

Address(a[i][j]) = Base Address + (j * m + i) * Element Size

Where:

• Base Address (BA) is the memory address of the first element a[0][0].
• i is the row index, j is the column index.
• m is the number of rows in the array.
• Element Size is the amount of memory required to store a single element.

Example Calculation:
If a[3][3] starts at the base address 1000 with Element Size 4 bytes, the address of a[1][2] in column-major order would be:

Address(a[1][2]) = 1000 + (2 * 3 + 1) * 4 = 1000 + (7 * 4) = 1000 + 28 = 1028

Thus, a[1][2] is stored at memory address 1028 in column-major order.

Applications of 2D to 1D Mapping

Understanding 2D to 1D array mapping is crucial in several applications:

• Graphics programming, where image data is often stored in 1D form, with pixels arranged row by row or column by column.
• Scientific computing, which deals with large matrices for simulations, data analysis, and matrix operations, particularly in data structures and database implementations.
• Machine learning, where tensors (multi-dimensional arrays) are mapped into 1D arrays for memory efficiency.

Advantages of Row and Column Major Orders

• Row Major Order is efficient for algorithms that process data row-wise, such as in linear algebra and image processing.
• Column Major Order is beneficial for matrix operations in data science and numerical computing languages that operate on columns efficiently.

Example Using 3×3 Matrix

Here’s an example using a 3×3 matrix with each element labeled by its row and column indices:

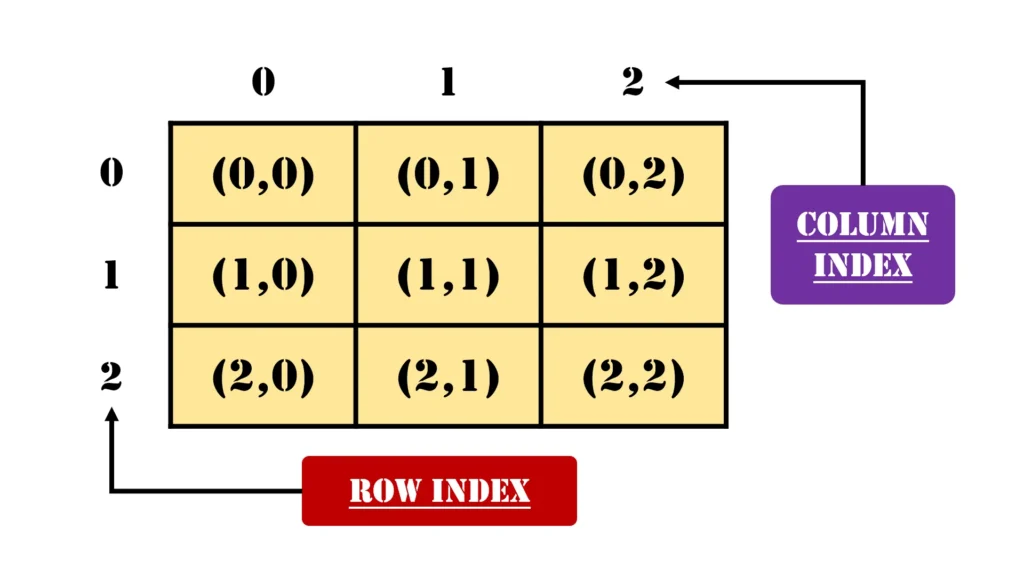
Matrix:

(0,0)  (0,1)  (0,2)
(1,0)  (1,1)  (1,2)
(2,0)  (2,1)  (2,2)

To store this matrix in memory as a 1D array, we can use Row Major Order or Column Major Order.

Row Major Order Example

In Row Major Order, we store elements row by row. So, for the above matrix, the elements in memory would look like this:

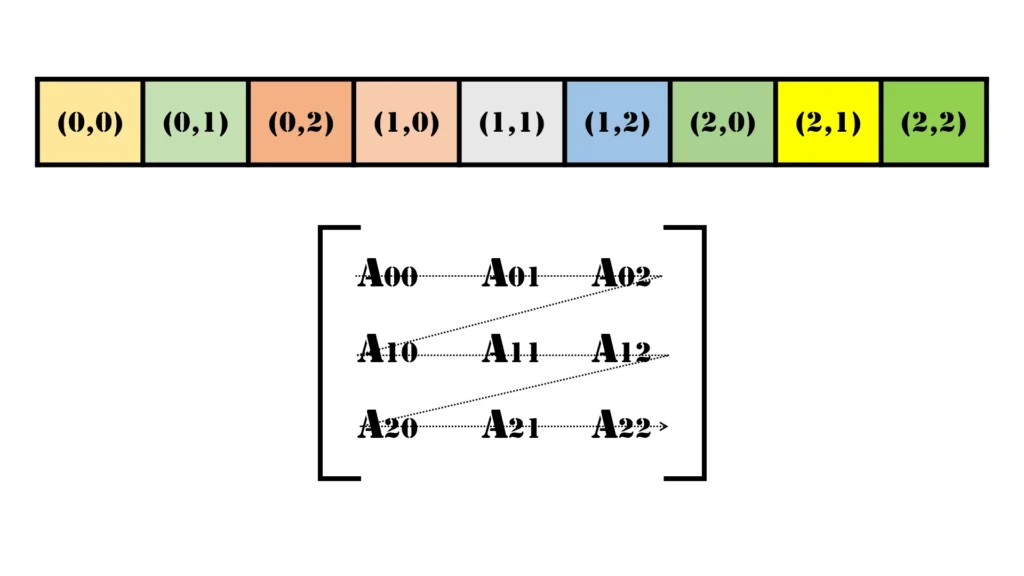
[(0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), (2,2)]

Each element gets assigned a position (index) in the 1D array:

• Index 0: (0,0)
• Index 1: (0,1)
• Index 2: (0,2)
• Index 3: (1,0)
• Index 4: (1,1)
• Index 5: (1,2)
• Index 6: (2,0)
• Index 7: (2,1)
• Index 8: (2,2)

Formula for Row Major Order

To calculate the position of an element at a[i][j] in a 1D array:

Index = i * number of columns + j

Examples:

• For (1,1): Index = 1 * 3 + 1 = 4
• For (2,0): Index = 2 * 3 + 0 = 6

Column Major Order Example

In Column Major Order, we store elements column by column. For this matrix, the 1D array in memory would look like this:

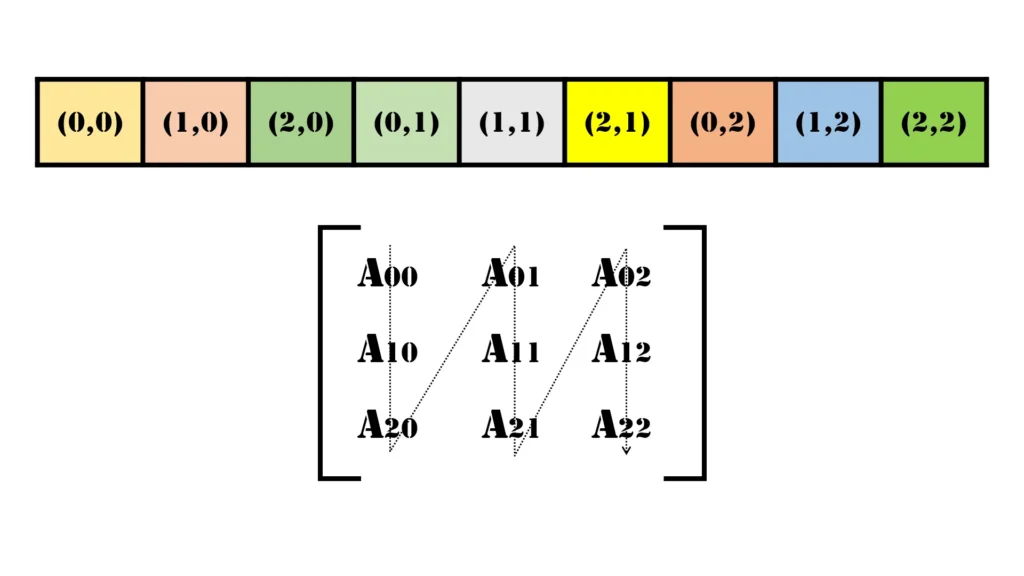
[(0,0), (1,0), (2,0), (0,1), (1,1), (2,1), (0,2), (1,2), (2,2)]

Here, each element is stored based on its column order, and the 1D index assignments are:

• Index 0: (0,0)
• Index 1: (1,0)
• Index 2: (2,0)
• Index 3: (0,1)
• Index 4: (1,1)
• Index 5: (2,1)
• Index 6: (0,2)
• Index 7: (1,2)
• Index 8: (2,2)

Formula for Column Major Order:

To calculate the position of an element at a[i][j] in a 1D array:

Index = j * number of rows + i

Examples:

• For (1,1): Index = 1 * 3 + 1 = 4
• For (2,0): Index = 0 * 3 + 2 = 2

Summary of Both Orders

• Row Major Order: [(0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), (2,2)]
• Column Major Order: [(0,0), (1,0), (2,0), (0,1), (1,1), (2,1), (0,2), (1,2), (2,2)]

This demonstrates how the memory layout differs depending on whether Row Major Order or Column Major Order is used.

In summary, mapping 2D arrays to 1D enables us to work within the constraints of linear memory structures. By carefully choosing row-major or column-major order based on the application, we can optimize performance and memory usage. Understanding these techniques and their application is essential for efficient programming, particularly in languages and fields that require direct memory management.

Frequently Asked Questions (FAQs) on Mapping 2D Arrays to 1D Arrays

Why do we need to map a 2D array to a 1D array?

Mapping a 2D array to a 1D array is necessary because computer memory is structured linearly. Even though 2D arrays appear as grids to us, they are stored sequentially in memory. Converting 2D arrays into a 1D format allows us to arrange elements contiguously, making data access faster and more memory efficient. Additionally, direct memory management (especially in low-level languages like C) requires us to compute the exact memory addresses of elements in linear memory, which is achieved using mapping techniques.

What are the main techniques for storing 2D arrays in memory?

There are two primary techniques for storing 2D arrays in memory: Row Major Order and Column Major Order.

• Row Major Order: Stores the array’s rows contiguously in memory, meaning all elements of the first row are stored first, followed by the second row, and so on.
• Column Major Order: Stores the array’s columns contiguously, so the first column is stored entirely first, followed by the second column, and so on.

These techniques are foundational in programming and determine how memory addresses for 2D arrays are computed based on row or column indices.

What is Row Major Order in 2D array mapping?

Row Major Order is a way of storing 2D arrays where all elements of each row are stored sequentially in memory. For example, if you have a 3 x 3 matrix:

a[3][3] = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

The array would be stored as [1, 2, 3, 4, 5, 6, 7, 8, 9] in memory. In Row Major Order, we calculate the memory address of an element a[i][j] as:

Address(a[i][j]) = Base Address + (i * n + j) * Element Size

Where i is the row index, j is the column index, and n is the number of columns.

What is Column Major Order in 2D array mapping?

Column Major Order is a storage technique where elements of each column are stored sequentially in memory. For the same 3 x 3 matrix example:

a[3][3] = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

The array would be stored as [1, 4, 7, 2, 5, 8, 3, 6, 9]. In Column Major Order, the memory address of an element a[i][j] is calculated as:

Address(a[i][j]) = Base Address + (j * m + i) * Element Size

Where i is the row index, j is the column index, and m is the number of rows.

How does memory address calculation differ in Row Major Order and Column Major Order?

In Row Major Order, the address of an element a[i][j] in a 2D array a[m][n] is calculated as:

Address(a[i][j]) = Base Address + (i * n + j) * Element Size

In Column Major Order, the address of an element a[i][j] is calculated as:

Address(a[i][j]) = Base Address + (j * m + i) * Element Size

The key difference is that Row Major Order focuses on rows (using the row index first), while Column Major Order focuses on columns (using the column index first). These formulas allow us to convert 2D indices into 1D memory addresses based on the chosen storage technique.

Which programming languages use Row Major Order or Column Major Order by default?

• Row Major Order: C and C++ use Row Major Order to store multi-dimensional arrays. This means that elements within a row are stored consecutively in memory.
• Column Major Order: Fortran and MATLAB use Column Major Order by default. This storage style is efficient for applications that perform operations on columns of data.

Choosing the appropriate language and storage order depends on the application requirements and the access patterns of the data.

What are some practical applications of 2D array to 1D array mapping?

Mapping 2D arrays to 1D arrays has numerous applications, especially in fields requiring matrix operations or multi-dimensional data handling:

• Graphics and Image Processing: 2D-pixel data is often mapped to a 1D structure for easier manipulation and storage.
• Scientific Computing: Matrices are frequently used in numerical simulations and data analysis, where efficient storage and access are crucial.
• Machine Learning: Tensors or multi-dimensional arrays are mapped into 1D arrays for memory efficiency, especially for large datasets.
• Database and Memory Management: Relational databases and data stored in table-like structures can benefit from efficient memory mapping.

How does Element Size affect memory address calculation?

Element Size represents the amount of memory required to store each array element (e.g., 4 bytes for an integer in many systems). This size factor is crucial in address calculations because it dictates how much space to move in memory to locate the next element.

In address calculation formulas:

• Row Major Order: Address(a[i][j]) = Base Address + (i * n + j) * Element Size
• Column Major Order: Address(a[i][j]) = Base Address + (j * m + i) * Element Size

Multiplying by Element Size ensures we reach the correct address, accounting for the space each element occupies in memory.

Are there advantages to choosing Row Major Order over Column Major Order, or vice versa?

Yes, each storage method has its advantages:

• Row Major Order is generally better for operations that iterate over rows, such as linear algebraic operations in languages like C and C++.
• Column Major Order is ideal for column-wise data access and is commonly used in scientific computing and data analysis languages like Fortran.

Choosing the right storage order depends on the data access patterns and the language used. If operations are frequently row-wise, Row Major Order will be more efficient; for column-based operations, Column Major Order is preferable.

Can we manually specify Row Major Order or Column Major Order in programming?

In many languages, the storage order is predefined by the language (e.g., Row Major in C/C++ and Column Major in Fortran/MATLAB). However, some languages and libraries (like NumPy in Python) allow users to specify storage order when creating multi-dimensional arrays. In NumPy, for instance, arrays can be set as C-contiguous (Row Major Order) or F-contiguous (Column Major Order), giving programmers flexibility based on their specific data needs.

Manually specifying storage order can optimize performance, especially in memory-intensive applications where access patterns matter.