Close Menu
Data Structures

Deletion at the End in Doubly Linked List: A Comprehensive Exploration

By

Managing data structures effectively is a cornerstone of computer science. Among the most versatile structures is the Doubly Linked List, which allows traversal in both forward and backward directions, making it a preferred choice for scenarios requiring efficient insertion and deletion. One common operation is deletion at the end of a doubly linked list. This operation, while seemingly simple, demands careful handling to ensure the integrity of the list.

In this article, we will discuss the algorithm, walk through its implementation in C, C++, C#, Java, JavaScript, and Python Programming Language, and provide insights into the time complexity and space complexity considerations. Let’s dive in step by step.

Deletion at the End in a Doubly Linked List
Deletion at the End in a Doubly Linked List

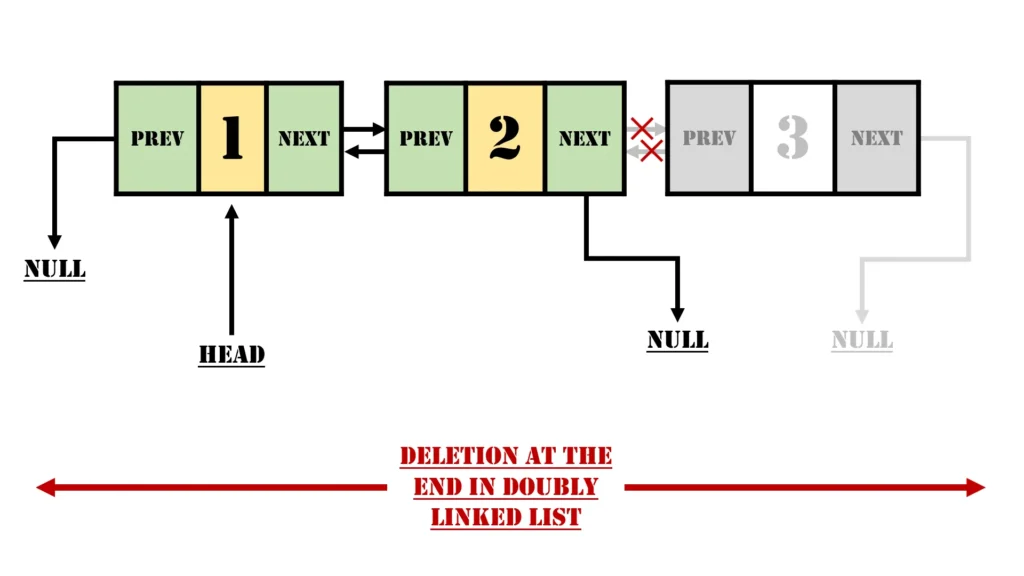
Understanding the Problem

A doubly linked list consists of nodes, each of which contains three components:

  • Data: The actual value stored in the node.
  • Next Pointer: A reference to the next node in the list.
  • Previous Pointer: A reference to the previous node.

Deletion of the last node, also known as the tail node, involves updating the pointer of the second-to-last node (often referred to as the penultimate node) to NULL and freeing the memory allocated to the tail node. This operation ensures the list remains intact and accessible even after the deletion.

Algorithm for Deleting the Last Node

The process for deleting the last node in a doubly linked list can be broken down into a series of logical steps:

Step 1: Check if the List is Empty

Before performing any operation, verify if the list exists. If the head pointer is NULL, it implies the list is empty, and there’s nothing to delete.

Step 2: Handle Single Node Lists

If the list contains only one node (i.e., the head’s next pointer is NULL), deleting this single node involves freeing its memory and setting the head pointer to NULL.

Step 3: Traverse to the Tail Node

If the list has multiple nodes, start at the head and traverse through the list until reaching the node whose next pointer is NULL. This is the tail node, which needs to be removed.

Step 4: Update the Penultimate Node

Modify the next pointer of the penultimate node (node before the tail) to NULL, thereby detaching the tail node from the list.

Step 5: Free the Tail Node

Deallocate the memory assigned to the tail node using the free function, ensuring there are no memory leaks.

Step 6: Return the Updated Head

Finally, return the updated head pointer, which might have been modified in case the list initially had only one node.

Implementation in C Programming Language

The above algorithm is implemented in C, as shown in the code below. This implementation handles all edge cases, including empty lists and single-node lists.

#include <stdio.h>
#include <stdlib.h>

// Define the structure for the doubly linked list node
struct Node {
    int data;            // Data stored in the node
    struct Node* prev;   // Pointer to the previous node
    struct Node* next;   // Pointer to the next node
};

// Function to delete the last node of the doubly linked list
struct Node* delLast(struct Node *head) {
    if (head == NULL)  // Case 1: If the list is empty, return NULL
        return NULL;
    if (head->next == NULL) {  // Case 2: If there is only one node in the list
        free(head);   // Free the only node
        return NULL;  // Return NULL as the list is now empty
    }

    // Traverse the list to find the last node
    struct Node *curr = head;
    while (curr->next != NULL)  // Move to the last node
        curr = curr->next;

    // Update the second-to-last node's next pointer
    curr->prev->next = NULL;

    // Free the memory of the last node
    free(curr);

    // Return the updated head of the list
    return head;
}

// Function to print the list
void printList(struct Node *head) {
    struct Node *curr = head;
    while (curr != NULL) {
        printf("%d ", curr->data);  // Print data of the current node
        curr = curr->next;          // Move to the next node
    }
    printf("\n");  // Print a newline after the list is printed
}

// Function to create a new node with the given data
struct Node* createNode(int data) {
    struct Node *newNode = (struct Node*)malloc(sizeof(struct Node));  // Allocate memory for the new node
    newNode->data = data;  // Set the data of the node
    newNode->prev = NULL;   // Set the previous pointer to NULL
    newNode->next = NULL;   // Set the next pointer to NULL
    return newNode;         // Return the newly created node
}

int main() {
    // Create a hardcoded doubly linked list: 1 <-> 2 <-> 3
    struct Node *head = createNode(1);        // Create the first node
    head->next = createNode(2);               // Create the second node and link it
    head->next->prev = head;                  // Set the previous pointer of the second node
    head->next->next = createNode(3);         // Create the third node and link it
    head->next->next->prev = head->next;      // Set the previous pointer of the third node

    head = delLast(head);  // Delete the last node
    printList(head);       // Print the updated list

    return 0;
}

Output:

Upon executing the above program with the hardcoded list 1 <-> 2 <-> 3, the following output is produced after deleting the last node:

1 2

This confirms that the last node (3) has been successfully removed, and the list remains intact.

Detailed Explanation of the Code

Node Structure

The structure struct Node defines the blueprint for each node in the list. It contains:

  • An integer data for storing the node value.
  • Two pointers: prev and next to connect the node to its neighbors.

delLast Function

  • Edge Case Handling:
    • If head == NULL, the list is empty, and the function returns NULL.
    • If head->next == NULL, it indicates a single-node list. The node is freed, and NULL is returned.
  • Traversal:
    • Starting from head, the curr pointer is moved to the last node by following curr->next until NULL.
  • Updating Pointers:
    • The penultimate node’s next pointer is updated to NULL to detach the tail node.
  • Freeing Memory:
    • The memory of the detached node is freed using the free function.
  • Return:
    • The head pointer, potentially updated, is returned.

Utility Functions

  • createNode: Dynamically allocates memory for a new node and initializes its data and pointers.
  • printList: Iterates through the list from the head and prints the data in each node.

Code Implementation In Multiple Programming Language

Here is the code written in C, C++, C#, Java, JavaScript, and Python, along with a detailed step-by-step explanation for each language.

Deletion at the End in a Doubly Linked List
Deletion at the End in a Doubly Linked List

C Program Implementation

#include <stdio.h>
#include <stdlib.h>

// Define the structure for the doubly linked list node
struct Node {
    int data;            // Data stored in the node
    struct Node* prev;   // Pointer to the previous node
    struct Node* next;   // Pointer to the next node
};

// Function to delete the last node of the doubly linked list
struct Node* delLast(struct Node *head) {
    if (head == NULL)  // Case 1: If the list is empty, return NULL
        return NULL;
    if (head->next == NULL) {  // Case 2: If there is only one node in the list
        free(head);   // Free the only node
        return NULL;  // Return NULL as the list is now empty
    }

    // Traverse the list to find the last node
    struct Node *curr = head;
    while (curr->next != NULL)  // Move to the last node
        curr = curr->next;

    // Update the second-to-last node's next pointer
    curr->prev->next = NULL;

    // Free the memory of the last node
    free(curr);

    // Return the updated head of the list
    return head;
}

// Function to print the list
void printList(struct Node *head) {
    struct Node *curr = head;
    while (curr != NULL) {
        printf("%d ", curr->data);  // Print data of the current node
        curr = curr->next;          // Move to the next node
    }
    printf("\n");  // Print a newline after the list is printed
}

// Function to create a new node with the given data
struct Node* createNode(int data) {
    struct Node *newNode = (struct Node*)malloc(sizeof(struct Node));  // Allocate memory for the new node
    newNode->data = data;  // Set the data of the node
    newNode->prev = NULL;   // Set the previous pointer to NULL
    newNode->next = NULL;   // Set the next pointer to NULL
    return newNode;         // Return the newly created node
}

int main() {
    // Create a hardcoded doubly linked list: 1 <-> 2 <-> 3
    struct Node *head = createNode(1);        // Create the first node
    head->next = createNode(2);               // Create the second node and link it
    head->next->prev = head;                  // Set the previous pointer of the second node
    head->next->next = createNode(3);         // Create the third node and link it
    head->next->next->prev = head->next;      // Set the previous pointer of the third node

    head = delLast(head);  // Delete the last node
    printList(head);       // Print the updated list

    return 0;
}

C++ Implementation

#include <iostream>
using namespace std;

// Define the structure for the doubly linked list node
struct Node {
    int data;            // Data stored in the node
    Node* prev;          // Pointer to the previous node
    Node* next;          // Pointer to the next node
};

// Function to delete the last node of the doubly linked list
Node* delLast(Node* head) {
    if (head == nullptr)  // Case 1: If the list is empty, return nullptr
        return nullptr;
    if (head->next == nullptr) {  // Case 2: If there is only one node
        delete head;              // Delete the only node
        return nullptr;           // Return nullptr as the list is now empty
    }

    // Traverse to the last node
    Node* curr = head;
    while (curr->next != nullptr)
        curr = curr->next;

    // Update the second-to-last node's next pointer
    curr->prev->next = nullptr;

    // Delete the last node
    delete curr;

    return head;  // Return the updated head of the list
}

// Function to print the list
void printList(Node* head) {
    Node* curr = head;
    while (curr != nullptr) {
        cout << curr->data << " ";  // Print the data of the current node
        curr = curr->next;          // Move to the next node
    }
    cout << endl;  // Print a newline after the list is printed
}

// Function to create a new node
Node* createNode(int data) {
    Node* newNode = new Node();  // Allocate memory for the new node
    newNode->data = data;        // Set the data of the node
    newNode->prev = nullptr;     // Set the previous pointer to nullptr
    newNode->next = nullptr;     // Set the next pointer to nullptr
    return newNode;              // Return the new node
}

int main() {
    // Create a hardcoded doubly linked list: 1 <-> 2 <-> 3
    Node* head = createNode(1);
    head->next = createNode(2);
    head->next->prev = head;
    head->next->next = createNode(3);
    head->next->next->prev = head->next;

    head = delLast(head);  // Delete the last node
    printList(head);       // Print the updated list

    return 0;
}

C# Implementation

using System;

// Define the structure for the doubly linked list node
class Node {
    public int Data;          // Data stored in the node
    public Node Prev;         // Pointer to the previous node
    public Node Next;         // Pointer to the next node

    // Constructor to create a new node
    public Node(int data) {
        Data = data;
        Prev = null;
        Next = null;
    }
}

class DoublyLinkedList {
    // Function to delete the last node
    public static Node DelLast(Node head) {
        if (head == null)  // Case 1: If the list is empty, return null
            return null;
        if (head.Next == null) {  // Case 2: If there is only one node
            head = null;          // Remove the only node
            return null;          // Return null as the list is now empty
        }

        // Traverse to the last node
        Node curr = head;
        while (curr.Next != null)
            curr = curr.Next;

        // Update the second-to-last node's next pointer
        curr.Prev.Next = null;

        // Return the updated head of the list
        return head;
    }

    // Function to print the list
    public static void PrintList(Node head) {
        Node curr = head;
        while (curr != null) {
            Console.Write(curr.Data + " ");  // Print the current node's data
            curr = curr.Next;               // Move to the next node
        }
        Console.WriteLine();  // Print a newline after the list
    }

    static void Main(string[] args) {
        // Create a hardcoded doubly linked list: 1 <-> 2 <-> 3
        Node head = new Node(1);
        head.Next = new Node(2);
        head.Next.Prev = head;
        head.Next.Next = new Node(3);
        head.Next.Next.Prev = head.Next;

        head = DelLast(head);  // Delete the last node
        PrintList(head);       // Print the updated list
    }
}

Java Implementation

public class DoublyLinkedList {
    // Define the structure for the doubly linked list node
    static class Node {
        int data;       // Data stored in the node
        Node prev;      // Pointer to the previous node
        Node next;      // Pointer to the next node

        // Constructor to create a new node
        Node(int data) {
            this.data = data;
            this.prev = null;
            this.next = null;
        }
    }

    // Function to delete the last node
    static Node delLast(Node head) {
        if (head == null)  // Case 1: If the list is empty, return null
            return null;
        if (head.next == null) {  // Case 2: If there is only one node
            head = null;          // Remove the only node
            return null;          // Return null as the list is now empty
        }

        // Traverse to the last node
        Node curr = head;
        while (curr.next != null)
            curr = curr.next;

        // Update the second-to-last node's next pointer
        curr.prev.next = null;

        // Return the updated head of the list
        return head;
    }

    // Function to print the list
    static void printList(Node head) {
        Node curr = head;
        while (curr != null) {
            System.out.print(curr.data + " ");  // Print the current node's data
            curr = curr.next;                  // Move to the next node
        }
        System.out.println();  // Print a newline after the list
    }

    public static void main(String[] args) {
        // Create a hardcoded doubly linked list: 1 <-> 2 <-> 3
        Node head = new Node(1);
        head.next = new Node(2);
        head.next.prev = head;
        head.next.next = new Node(3);
        head.next.next.prev = head.next;

        head = delLast(head);  // Delete the last node
        printList(head);       // Print the updated list
    }
}

JavaScript Implementation

// Define the Node class for a doubly linked list
class Node {
    constructor(data) {
        this.data = data;  // Data stored in the node
        this.prev = null;  // Pointer to the previous node
        this.next = null;  // Pointer to the next node
    }
}

// Function to delete the last node
function delLast(head) {
    if (head === null)  // Case 1: If the list is empty, return null
        return null;
    if (head.next === null) {  // Case 2: If there is only one node
        head = null;           // Remove the only node
        return null;           // Return null as the list is now empty
    }

    // Traverse to the last node
    let curr = head;
    while (curr.next !== null)
        curr = curr.next;

    // Update the second-to-last node's next pointer
    curr.prev.next = null;

    // Return the updated head of the list
    return head;
}

// Function to print the list
function printList(head) {
    let curr = head;
    while (curr !== null) {
        process.stdout.write(curr.data + " ");  // Print the current node's data
        curr = curr.next;                      // Move to the next node
    }
    console.log();  // Print a newline after the list
}

// Create a hardcoded doubly linked list: 1 <-> 2 <-> 3
let head = new Node(1);
head.next = new Node(2);
head.next.prev = head;
head.next.next = new Node(3);
head.next.next.prev = head.next;

head = delLast(head);  // Delete the last node
printList(head);       // Print the updated list

Python Implementation

# Define the Node class for a doubly linked list
class Node:
    def __init__(self, data):
        self.data = data  # Data stored in the node
        self.prev = None  # Pointer to the previous node
        self.next = None  # Pointer to the next node

# Function to delete the last node
def delLast(head):
    if head is None:  # Case 1: If the list is empty, return None
        return None
    if head.next is None:  # Case 2: If there is only one node
        head = None        # Remove the only node
        return None

    # Traverse to the last node
    curr = head
    while curr.next is not None:
        curr = curr.next

    # Update the second-to-last node's next pointer
    curr.prev.next = None

    # Return the updated head of the list
    return head

# Function to print the list
def printList(head):
    curr = head
    while curr:
        print(curr.data, end=" ")  # Print the current node's data
        curr = curr.next           # Move to the next node
    print()  # Print a newline after the list

# Create a hardcoded doubly linked list: 1 <-> 2 <-> 3
head = Node(1)
head.next = Node(2)
head.next.prev = head
head.next.next = Node(3)
head.next.next.prev = head.next

head = delLast(head)  # Delete the last node
printList(head)       # Print the updated list

Output:

Upon executing the above program with the hardcoded list 1 <-> 2 <-> 3, the following output is produced after deleting the last node:

1 2

Time and Space Complexity

  • Time Complexity:
    Traversing the list to locate the tail node requires O(n) operations, where n is the number of nodes in the list. Other operations, such as pointer updates and memory deallocation, are O(1).
  • Auxiliary Space:
    The operation uses no additional data structures, making the space complexity O(1).

Advantages of Deletion at the End in Doubly Linked List

  • Efficient Traversal
    • Two-way navigation in a doubly linked list simplifies the deletion process at the end.
    • Unlike a Singly Linked List, there is no need to traverse the entire list to find the second-to-last node. You can directly use the prev pointer of the last node.
  • No Wasted Memory
    • Only the last node is freed, and the rest of the nodes remain intact, ensuring efficient memory usage.
    • The doubly linked list does not require additional temporary variables or extensive memory management during deletion.
  • Supports Dynamic Size
    • In contrast to arrays, a doubly linked list dynamically adjusts its size during deletion.
    • Deletion at the end does not require shifting of elements, which can be computationally expensive in other data structures.
  • Flexibility in Modifying Adjacent Nodes
    • The prev pointer of the second-to-last node can be directly updated to NULL, making the operation more straightforward and efficient.
  • Improved Performance in Certain Applications
    • Deletion at the end is particularly useful in scenarios such as:
      • Stacks: Removing the topmost element in a stack implemented using a doubly linked list.
      • Deque (Double-Ended Queue): Deleting from the rear of the deque efficiently.
    • These applications benefit from the direct access provided by the prev pointer.
  • No Need for Reallocation
    • Deletion in a doubly linked list avoids the need to reallocate or resize memory blocks, unlike dynamic arrays.
  • Simpler Algorithm for Tail Deletion
    • With a doubly linked list, the algorithm for deleting the last node is shorter and cleaner due to the prev pointer, making it easier to implement and debug.
  • Robustness for Complex Operations
    • Doubly linked lists are preferred in operations that require repeated insertions and deletions at both ends, making them ideal for:
      • Cache implementations (e.g., LRU Cache) where tail deletion is frequently required.
      • History tracking systems, where operations at both ends of the list are common.
  • Maintains Data Integrity
    • By properly updating pointers, the operation ensures that the structure of the list remains intact.
    • There is no risk of “dangling pointers” if the node to be deleted is correctly freed.
  • Ease of Handling Edge Cases
    • Special cases like deleting the only node in the list or an empty list can be handled efficiently.
      • In an empty list: Simply return NULL.
      • In a single-node list: Free the node and set the head to NULL.
    • These cases are straightforward in doubly linked lists due to their bidirectional pointers.

Conclusion

The deletion of the last node in a doubly linked list is a straightforward yet crucial operation in various applications, from memory management to dynamic data structures. By carefully handling edge cases and ensuring proper memory management, the C program provided serves as a robust solution for this task. The knowledge of such operations is essential for mastering linked list manipulation and can pave the way for tackling more complex data structures and algorithms.

  1. Deletion in a Doubly Linked List with Implementation: A Comprehensive Guide
  2. Deletion at the Beginning in a Doubly Linked List: A Detailed Exploration
  3. Deletion after a given node in Doubly Linked List: A Comprehensive Guide
  4. Deleting a Node Before a Given Node in a Doubly Linked List: A Detailed Exploration
  5. Deletion at a Specific Position in a Doubly Linked List: A Detailed Exploration
  6. Deletion at the End in Doubly Linked List: A Comprehensive Exploration

Frequently Asked Questions (FAQs)

What is a Doubly Linked List, and how does it differ from a Singly Linked List?

A Doubly Linked List (DLL) is a type of linked data structure where each node contains three components:

  • Data: The value stored in the node.
  • Next Pointer: A reference to the next node in the list.
  • Previous Pointer: A reference to the previous node in the list.

In contrast, a Singly Linked List (SLL) contains nodes with only two components:

  • Data: The value stored in the node.
  • Next Pointer: A reference to the next node.

Key Differences:

  • Traversal: In a DLL, traversal can occur both forward and backward, while an SLL only supports forward traversal.
  • Memory Overhead: A DLL uses more memory due to the additional pointer (prev) in each node.
  • Insertion/Deletion: In a DLL, insertion, and deletion are more flexible since both forward and backward references are available, unlike in an SLL, where you need to traverse to find the previous node for certain operations.

Why is Deletion at the End a Common Operation in Doubly Linked Lists?

Deletion at the end is a frequent operation in doubly linked lists due to their dynamic nature. Some common scenarios include:

  • Memory Management: Removing unused or unnecessary nodes to free memory.
  • Dynamic Data Structures: Lists that grow and shrink dynamically, such as stacks implemented using linked lists.
  • Efficient Updates: In DLLs, the backward traversal allows easy access to the penultimate node, making the operation more efficient compared to an SLL.

How Does the delLast Function Handle Empty Lists in the Implementation?

The delLast function begins by checking if the list is empty:

if (head == NULL)
    return NULL;

If the head pointer is NULL, it indicates that the list is empty. In this case, the function simply returns NULL, as there is no node to delete. This is a critical step to avoid segmentation faults or undefined behavior.

How Are Single-Node Lists Treated Differently in the delLast Function?

If the list contains only one node, i.e., when head->next == NULL, the delLast function takes the following actions:

  • Frees the memory allocated for the single node: free(head);
  • Updates the head pointer to NULL to indicate that the list is now empty: return NULL;

This special handling is necessary because there is no penultimate node to update, and failure to set head to NULL would leave a dangling pointer.

How Does the delLast Function Traverse to the Last Node?

The function uses a while loop to traverse the list:

struct Node *curr = head;
while (curr->next != NULL)
    curr = curr->next;

Here’s what happens step by step:

  • The curr pointer is initialized to the head of the list.
  • The loop iterates until curr->next becomes NULL, indicating the last node.
  • At the end of the loop, curr points to the last node (tail).

This traversal has a time complexity of O(n), where n is the number of nodes in the list.

How Is the Penultimate Node Updated in the delLast Function?

Once the tail node is identified using traversal, its predecessor (penultimate node) is updated:

curr->prev->next = NULL;

This step ensures that the penultimate node’s next pointer no longer references the now-deleted tail node. As a result, the list remains intact and terminates correctly.

Why Is the Free Function Important in the delLast Implementation?

The free function is used to release the memory allocated for the node being deleted:

free(curr);

Importance:

  • Memory Management: Prevents memory leaks by ensuring the dynamically allocated memory is returned to the system.
  • Efficiency: Makes the program more resource-efficient, especially for applications that involve frequent deletions.

Failing to use free results in memory leaks, where unused memory remains allocated, potentially causing the system to run out of memory over time.

What Does the printList Function Do, and Why Is It Useful?

The printList function iterates through the doubly linked list and prints the data in each node:

void printList(struct Node *head) {
    struct Node *curr = head;
    while (curr != NULL) {
        printf("%d ", curr->data);
        curr = curr->next;
    }
    printf("\n");
}

Utility:

  • Debugging: Helps verify that the list structure remains intact after operations like deletion.
  • Visualization: Provides a clear view of the list’s current state.

For example, after deleting the last node from 1 <-> 2 <-> 3, the printList function outputs:

1 2

What Are the Time and Space Complexities of Deletion at the End in a Doubly Linked List?

Time Complexity:

  • The traversal to find the tail node takes O(n), where n is the number of nodes in the list.
  • Updating the pointers and freeing the memory are constant-time operations, O(1).
  • Overall time complexity: O(n).

Space Complexity:

  • No additional data structures are used.
  • The operation modifies existing pointers, making the auxiliary space usage O(1).

Can You Summarize the Edge Cases Addressed by the delLast Function?

The delLast function addresses the following edge cases:

  • Empty List:
    • If the list is empty (head == NULL), it simply returns NULL.
  • Single-Node List:
    • If the list contains only one node (head->next == NULL), it frees the node and updates the head pointer to NULL.
  • Multi-Node List:
    • It traverses to the last node, updates the penultimate node’s next pointer to NULL, and frees the memory of the tail node.
  • Memory Management:
    • Ensures no memory leaks by freeing dynamically allocated memory for deleted nodes.

These considerations make the function robust and suitable for practical applications.

Share.
Examsmeta Logo

Examsmeta serves as a comprehensive hub for educational resources across diverse disciplines. Designed to deliver high-quality, topic-wise notes and articles, it caters to students, educators, researchers, and lifelong learners. The goal is to make learning accessible, engaging, and effective for all. With a focus on providing detailed, accurate, and up-to-date content, Examsmeta fosters a passion for learning and supports both academic and professional growth. Whether it's exam preparation, research, or knowledge expansion, this platform offers guidance every step of the way.