Close Menu
Data Structures

Deleting a Node Before a Given Node in a Doubly Linked List: A Detailed Exploration

By

Doubly linked lists are a fundamental data structure in computer science, characterized by their bidirectional traversal capability. Each node in a doubly linked list contains three elements: the data, a pointer to the next node, and a pointer to the previous node. This unique structure allows for more flexibility compared to singly linked lists, such as easier deletion and insertion at both ends.

In this detailed post, we will explore how to delete a node before a specific node in a doubly linked list using a structured algorithm and then implement this algorithm in C programming language. We’ll also discuss the time complexity, auxiliary space, and nuances of the process.

Understanding the Problem

Deletion Before a Given Node in a Doubly Linked List
Deletion Before a Given Node in a Doubly Linked List

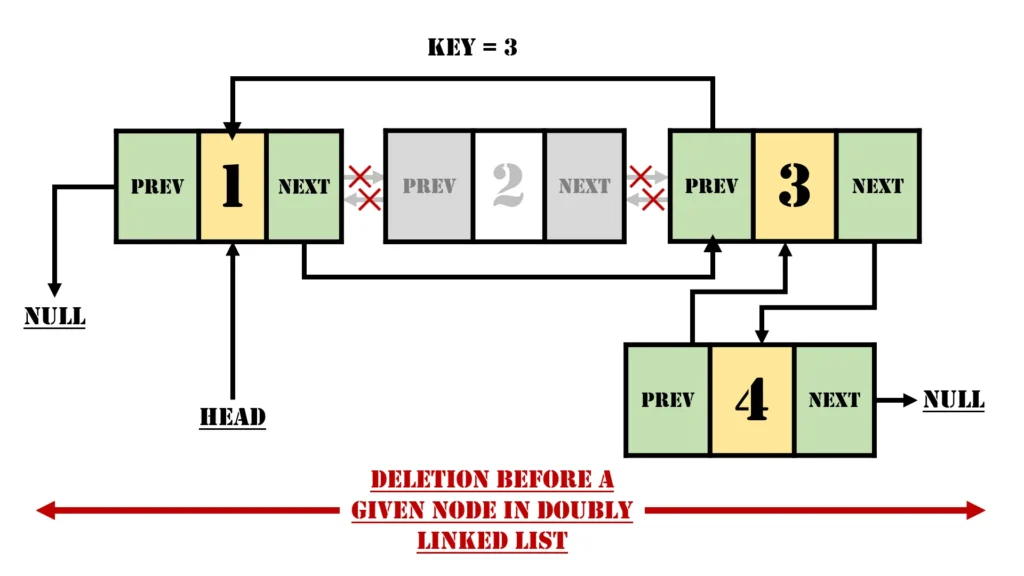
The task is to delete a node preceding a specific node in a doubly linked list. Consider a doubly linked list as:

Head <-> 1 <-> 2 <-> 3 <-> 4 <-> NULL

If the target node (key) is 3, we need to delete the node before it, i.e., the node 2. Post-deletion, the list should become:

Head <-> 1 <-> 3 <-> 4 <-> NULL

This operation has several scenarios:

  • Node to be deleted does not exist (for example, when the specified node is the head or its prev pointer is NULL).
  • Node to be deleted is the head node (special handling is required).
  • General case where the preceding node exists and needs to be deleted.

Step-by-Step Algorithm

The process of deleting a node before a specified node is straightforward but requires careful attention to pointers:

  • Locate the Target Node: Traverse the doubly linked list to find the node with the given key value.
  • Check Deletion Eligibility:
    • If the target node or its prev pointer is NULL, the operation cannot proceed because there is no preceding node to delete.
  • Set Up Pointers for Deletion:
    • Identify the node to be deleted (nodeToDelete) as the node pointed to by the prev pointer of the target node.
    • Update the prev pointer of the target node to point to the node preceding nodeToDelete.
    • If nodeToDelete is not the head, update the next pointer of its previous node to point to the target node.
  • Delete the Node: Free the memory allocated to the node to ensure there are no memory leaks.

Code Implementation in C Programming

Below is the C implementation of the described algorithm:

#include <stdio.h>
#include <stdlib.h>

// Definition of a Node in a Doubly Linked List
struct Node {
    int data;
    struct Node *next;
    struct Node *prev;
};

// Function to delete a node before a given node
struct Node *deleteBefore(struct Node *head, int key) {
    struct Node *curr = head;

    // Traverse the list to find the target node
    while (curr != NULL) {
        if (curr->data == key)
            break;
        curr = curr->next;
    }

    // Check if there is no node to delete
    if (curr == NULL || curr->prev == NULL)
        return head;

    // Node to be deleted
    struct Node *nodeToDelete = curr->prev;

    // Update the pointers to bypass the node to be deleted
    curr->prev = nodeToDelete->prev;

    if (nodeToDelete->prev != NULL) {
        nodeToDelete->prev->next = curr;
    } else {
        // Update head if the head node is deleted
        head = curr;
    }

    // Free the memory occupied by the node to be deleted
    free(nodeToDelete);

    return head;
}

// Function to print the Doubly Linked List
void printList(struct Node *head) {
    struct Node *curr = head;
    while (curr != NULL) {
        printf(" %d", curr->data);
        curr = curr->next;
    }
    printf("\n");
}

// Helper function to create a new node
struct Node *createNode(int new_data) {
    struct Node *new_node = (struct Node *)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = NULL;
    new_node->prev = NULL;
    return new_node;
}

// Driver Code
int main() {
    // Create a sample doubly linked list: 1 <-> 2 <-> 3 <-> 4
    struct Node *head = createNode(1);
    head->next = createNode(2);
    head->next->prev = head;
    head->next->next = createNode(3);
    head->next->next->prev = head->next;
    head->next->next->next = createNode(4);
    head->next->next->next->prev = head->next->next;

    printf("Original List:");
    printList(head);

    // Delete the node before the node with value 3
    head = deleteBefore(head, 3);

    printf("Updated List:");
    printList(head);

    return 0;
}

Output:

When the above code is executed, it produces the following output:

Original List: 1 2 3 4
Updated List: 1 3 4

Key Observations:

  • The node with data 2 is successfully deleted because it precedes the node with data 3.
  • The head pointer is appropriately updated if the head node is deleted, ensuring the list’s integrity.

Code Walkthrough

  • Node Creation: The createNode function dynamically allocates memory for new nodes and initializes their data, next, and prev pointers.
  • Linked List Setup: The main function hardcodes a doubly linked list with four nodes for demonstration purposes.
  • Deletion Function: The deleteBefore function performs the actual deletion logic based on the algorithm outlined above.
  • Output: The printList function traverses and displays the list before and after the deletion operation.

Code Implementation In Multiple Programming Languages

Here is the code written in C, C++, C#, Java, JavaScript, and Python, along with a detailed step-by-step explanation for each language.

Deletion Before a Given Node in a Doubly Linked List
Deletion Before a Given Node in a Doubly Linked List

C Program Implementation

#include <stdio.h>
#include <stdlib.h>

// Definition of a Node in a Doubly Linked List
struct Node {
    int data;
    struct Node *next;
    struct Node *prev;
};

// Function to delete a node before a given node
struct Node *deleteBefore(struct Node *head, int key) {
    struct Node *curr = head;

    // Traverse the list to find the node with the given key
    while (curr != NULL) {
        if (curr->data == key)
            break;
        curr = curr->next;
    }

    // If the key is not found or no node exists before the current node
    if (curr == NULL || curr->prev == NULL)
        return head;

    // Node to be deleted
    struct Node *nodeToDelete = curr->prev;

    // Update the 'prev' pointer of the current node to bypass the nodeToDelete
    curr->prev = nodeToDelete->prev;

    // If nodeToDelete is not the head node, update the next pointer of the previous node
    if (nodeToDelete->prev != NULL) {
        nodeToDelete->prev->next = curr;
    } else {
        // If nodeToDelete is the head node, update the head pointer
        head = curr;
    }

    // Free the memory occupied by nodeToDelete
    free(nodeToDelete);

    return head;
}

// Function to print the Doubly Linked List
void printList(struct Node *head) {
    struct Node *curr = head;
    while (curr != NULL) {
        printf(" %d", curr->data);
        curr = curr->next;
    }
    printf("\n");
}

// Helper function to create a new node
struct Node *createNode(int new_data) {
    struct Node *new_node = (struct Node *)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = NULL;
    new_node->prev = NULL;
    return new_node;
}

// Driver Code
int main() {
    // Create a sample doubly linked list: 1 <-> 2 <-> 3 <-> 4
    struct Node *head = createNode(1);
    head->next = createNode(2);
    head->next->prev = head;
    head->next->next = createNode(3);
    head->next->next->prev = head->next;
    head->next->next->next = createNode(4);
    head->next->next->next->prev = head->next->next;

    printf("Original List:");
    printList(head);

    // Delete the node before the node with value 3
    head = deleteBefore(head, 3);

    printf("Updated List:");
    printList(head);

    return 0;
}

C++ Implementation

#include <iostream>
using namespace std;

// Definition of a Node in a Doubly Linked List
struct Node {
    int data;
    Node *next;
    Node *prev;
};

// Function to delete a node before a given node
Node* deleteBefore(Node* head, int key) {
    Node* curr = head;

    // Traverse the list to find the target node
    while (curr != nullptr) {
        if (curr->data == key)
            break;
        curr = curr->next;
    }

    // Check if there is no node to delete
    if (curr == nullptr || curr->prev == nullptr)
        return head;

    // Node to be deleted
    Node* nodeToDelete = curr->prev;

    // Update the pointers to bypass the node to be deleted
    curr->prev = nodeToDelete->prev;

    if (nodeToDelete->prev != nullptr) {
        nodeToDelete->prev->next = curr;
    } else {
        // Update head if the head node is deleted
        head = curr;
    }

    // Free the memory occupied by the node to be deleted
    delete nodeToDelete;

    return head;
}

// Function to print the Doubly Linked List
void printList(Node* head) {
    Node* curr = head;
    while (curr != nullptr) {
        cout << " " << curr->data;
        curr = curr->next;
    }
    cout << endl;
}

// Helper function to create a new node
Node* createNode(int new_data) {
    Node* new_node = new Node();
    new_node->data = new_data;
    new_node->next = nullptr;
    new_node->prev = nullptr;
    return new_node;
}

// Driver Code
int main() {
    // Create a sample doubly linked list: 1 <-> 2 <-> 3 <-> 4
    Node* head = createNode(1);
    head->next = createNode(2);
    head->next->prev = head;
    head->next->next = createNode(3);
    head->next->next->prev = head->next;
    head->next->next->next = createNode(4);
    head->next->next->next->prev = head->next->next;

    cout << "Original List:";
    printList(head);

    // Delete the node before the node with value 3
    head = deleteBefore(head, 3);

    cout << "Updated List:";
    printList(head);

    return 0;
}

C# Implementation

using System;

class Node {
    public int data;
    public Node next;
    public Node prev;

    public Node(int data) {
        this.data = data;
        next = null;
        prev = null;
    }
}

class DoublyLinkedList {
    public static Node DeleteBefore(Node head, int key) {
        Node curr = head;

        // Traverse the list to find the target node
        while (curr != null) {
            if (curr.data == key)
                break;
            curr = curr.next;
        }

        // Check if there is no node to delete
        if (curr == null || curr.prev == null)
            return head;

        // Node to be deleted
        Node nodeToDelete = curr.prev;

        // Update the pointers to bypass the node to be deleted
        curr.prev = nodeToDelete.prev;

        if (nodeToDelete.prev != null) {
            nodeToDelete.prev.next = curr;
        } else {
            // Update head if the head node is deleted
            head = curr;
        }

        return head;
    }

    public static void PrintList(Node head) {
        Node curr = head;
        while (curr != null) {
            Console.Write(" " + curr.data);
            curr = curr.next;
        }
        Console.WriteLine();
    }

    public static void Main() {
        // Create a sample doubly linked list: 1 <-> 2 <-> 3 <-> 4
        Node head = new Node(1);
        head.next = new Node(2);
        head.next.prev = head;
        head.next.next = new Node(3);
        head.next.next.prev = head.next;
        head.next.next.next = new Node(4);
        head.next.next.next.prev = head.next.next;

        Console.WriteLine("Original List:");
        PrintList(head);

        // Delete the node before the node with value 3
        head = DeleteBefore(head, 3);

        Console.WriteLine("Updated List:");
        PrintList(head);
    }
}

Java Implementation

class Node {
    int data;
    Node next;
    Node prev;

    Node(int data) {
        this.data = data;
        next = null;
        prev = null;
    }
}

public class DoublyLinkedList {
    public static Node deleteBefore(Node head, int key) {
        Node curr = head;

        // Traverse the list to find the target node
        while (curr != null) {
            if (curr.data == key)
                break;
            curr = curr.next;
        }

        // Check if there is no node to delete
        if (curr == null || curr.prev == null)
            return head;

        // Node to be deleted
        Node nodeToDelete = curr.prev;

        // Update the pointers to bypass the node to be deleted
        curr.prev = nodeToDelete.prev;

        if (nodeToDelete.prev != null) {
            nodeToDelete.prev.next = curr;
        } else {
            // Update head if the head node is deleted
            head = curr;
        }

        return head;
    }

    public static void printList(Node head) {
        Node curr = head;
        while (curr != null) {
            System.out.print(" " + curr.data);
            curr = curr.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        // Create a sample doubly linked list: 1 <-> 2 <-> 3 <-> 4
        Node head = new Node(1);
        head.next = new Node(2);
        head.next.prev = head;
        head.next.next = new Node(3);
        head.next.next.prev = head.next;
        head.next.next.next = new Node(4);
        head.next.next.next.prev = head.next.next;

        System.out.println("Original List:");
        printList(head);

        // Delete the node before the node with value 3
        head = deleteBefore(head, 3);

        System.out.println("Updated List:");
        printList(head);
    }
}

JavaScript Implementation

class Node {
    constructor(data) {
        this.data = data;
        this.next = null;
        this.prev = null;
    }
}

function deleteBefore(head, key) {
    let curr = head;

    // Traverse the list to find the target node
    while (curr !== null) {
        if (curr.data === key) break;
        curr = curr.next;
    }

    // Check if there is no node to delete
    if (curr === null || curr.prev === null) return head;

    // Node to be deleted
    let nodeToDelete = curr.prev;

    // Update the pointers to bypass the node to be deleted
    curr.prev = nodeToDelete.prev;

    if (nodeToDelete.prev !== null) {
        nodeToDelete.prev.next = curr;
    } else {
        // Update head if the head node is deleted
        head = curr;
    }

    return head;
}

function printList(head) {
    let curr = head;
    while (curr !== null) {
        process.stdout.write(` ${curr.data}`);
        curr = curr.next;
    }
    console.log();
}

// Create a sample doubly linked list: 1 <-> 2 <-> 3 <-> 4
let head = new Node(1);
head.next = new Node(2);
head.next.prev = head;
head.next.next = new Node(3);
head.next.next.prev = head.next;
head.next.next.next = new Node(4);
head.next.next.next.prev = head.next.next;

console.log("Original List:");
printList(head);

// Delete the node before the node with value 3
head = deleteBefore(head, 3);

console.log("Updated List:");
printList(head);

Python Implementation

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None
        self.prev = None

def delete_before(head, key):
    curr = head

    # Traverse the list to find the target node
    while curr:
        if curr.data == key:
            break
        curr = curr.next

    # Check if there is no node to delete
    if curr is None or curr.prev is None:
        return head

    # Node to be deleted
    node_to_delete = curr.prev

    # Update the pointers to bypass the node to be deleted
    curr.prev = node_to_delete.prev

    if node_to_delete.prev:
        node_to_delete.prev.next = curr
    else:
        # Update head if the head node is deleted
        head = curr

    return head

def print_list(head):
    curr = head
    while curr:
        print(curr.data, end=" ")
        curr = curr.next
    print()

# Create a sample doubly linked list: 1 <-> 2 <-> 3 <-> 4
head = Node(1)
head.next = Node(2)
head.next.prev = head
head.next.next = Node(3)
head.next.next.prev = head.next
head.next.next.next = Node(4)
head.next.next.next.prev = head.next.next

print("Original List:")
print_list(head)

# Delete the node before the node with value 3
head = delete_before(head, 3)

print("Updated List:")
print_list(head)

Output:

Original List: 
1 2 3 4
Updated List: 
1 3 4

Time and Space Complexity

  • Time Complexity:
    • The deletion function traverses the list to locate the target node, resulting in an O(n) time complexity, where n is the number of nodes.
  • Auxiliary Space:
    • The space complexity is O(1) as no additional space is used apart from the pointers.

Advantages of Deleting a Node Before a Given Node in a Doubly Linked List

  • Flexibility in Node Manipulation
    • One of the most significant advantages of a doubly linked list is its flexibility in node manipulation, and deleting a node before a specific node demonstrates this perfectly. By using both prev and next pointers, you can easily traverse and update links to remove unnecessary or redundant nodes. This operation is not easily achievable in singly linked lists, where backward traversal is impossible.
  • Efficient Memory Management
    • Deleting unnecessary nodes before a given node optimizes memory usage. This is especially critical in systems with limited memory or those requiring real-time data updates, such as:
      • Embedded systems.
      • Dynamic caches. By deallocating memory for nodes no longer needed, you prevent memory leaks and ensure efficient use of system resources.
  • Simplified Code for Special Cases
    • In scenarios where a node needs to be deleted but cannot be accessed directly (e.g., it is not known whether a node exists before the given node), the algorithm simplifies operations:
      • If the target node is the head or its prev pointer is NULL, the operation terminates gracefully without additional conditions.
      • This avoids undefined behavior and ensures the integrity of the list.
  • Improved List Integrity
    • When nodes are dynamically inserted or removed, the structure of the list might become inconsistent if not handled properly. The ability to delete a node before a specific node ensures:
      • Correct updating of pointers (prev and next), maintaining the integrity of the list.
      • Seamless traversal in both directions after deletion, as the remaining nodes remain correctly linked.
  • Real-Time Use Cases
    • This operation is directly applicable in real-world scenarios where bidirectional traversal and selective deletion are critical:
      • Undo Functionality: In software where each user action is tracked (e.g., text editors), you might need to remove redundant actions dynamically.
      • Version Control Systems: Managing branches or revisions in systems like Git may involve removing unnecessary commits (nodes).
      • Media Playback Systems: Removing skipped or redundant media tracks while preserving the forward and backward navigation functionality.
  • Optimized Traversal and Search
    • By efficiently deleting a node, the doubly linked list becomes smaller, which reduces the time taken for subsequent traversals and searches. For example:
      • In a playlist application, removing skipped songs (nodes) minimizes traversal time to reach the desired song.
      • In network routing, deleting a less optimal route from the routing table can improve lookup efficiency.
  • Reusability of Deleted Nodes
    • In C programming and similar languages, freeing memory using free() makes the memory space available for reuse. This is particularly useful in environments where:
      • Memory is allocated dynamically using malloc().
      • The system handles large volumes of data and cannot afford memory wastage.
  • Bidirectional Traversal Benefits
    • The presence of the prev pointer in a doubly linked list makes backward traversal straightforward. Deleting a node before a given node is an operation that directly leverages this feature:
      • Without the prev pointer, determining the node before a given node would require an entire traversal from the head, increasing complexity.
      • This feature is unique to doubly linked lists, giving them an advantage over singly linked lists.
  • Scalability for Complex Applications
    • In larger applications, such as database management systems or data analytics tools, lists often grow dynamically. Deleting a node before a specific node is particularly advantageous in:
      • Data Cleanup: Removing outdated or redundant data points to keep datasets concise.
      • Dynamic Updates: Modifying lists in response to user actions or real-time system requirements.
  • Reduced Computational Overhead
    • Unlike array-based structures, where deletion requires shifting elements and resizing, deleting a node in a doubly linked list is efficient:
      • Only a few pointer adjustments are required.
      • There is no need to move other elements, as nodes are dynamically linked.

Conclusion

The ability to manipulate nodes in a doubly linked list provides versatility in various programming scenarios. The discussed algorithm for deleting a node before a given node is efficient and highlights the advantages of using doubly linked lists over singly linked lists for such operations. By carefully managing pointers and freeing memory, we ensure that the structure remains intact and there are no memory leaks.

  1. Deletion in a Doubly Linked List with Implementation: A Comprehensive Guide
  2. Deletion at the Beginning in a Doubly Linked List: A Detailed Exploration
  3. Deletion after a given node in Doubly Linked List: A Comprehensive Guide
  4. Deleting a Node Before a Given Node in a Doubly Linked List: A Detailed Exploration
  5. Deletion at a Specific Position in a Doubly Linked List: A Detailed Exploration
  6. Deletion at the End in Doubly Linked List: A Comprehensive Exploration

Frequently Asked Questions (FAQs)

What is a doubly linked list, and how is it different from a singly linked list?

A doubly linked list is a type of linked list where each node contains three elements:

  • Data: The actual value stored in the node.
  • Next Pointer: A pointer that refers to the next node in the list.
  • Previous Pointer: A pointer that refers to the previous node in the list.

The primary difference between doubly linked lists and singly linked lists is the presence of the previous pointer. In a singly linked list, each node only has a next pointer, making traversal unidirectional. In contrast, doubly linked lists allow bidirectional traversal, enabling more efficient insertions and deletions at both ends and intermediate positions.

Why would you need to delete a node before a specific node in a doubly linked list?

Deleting a node before a specific node is often required in various applications where precise control over the structure of a doubly linked list is necessary. For example:

  • Dynamic memory management in operating systems.
  • Undo functionality in applications that use doubly linked lists to track history.
  • Data compression or editing, where you might need to remove redundant or unnecessary nodes dynamically.

This operation ensures that the list remains optimized for traversal and manipulation, especially in large-scale or dynamic data systems.

What are the edge cases to consider when deleting a node before a specific node?

When performing this operation, the following edge cases must be handled carefully:

  • Target Node Not Found: If the specified node with the given key is not present in the list, no deletion should occur.
  • No Preceding Node: If the target node is the head node or its prev pointer is NULL, there is no node to delete before it.
  • Head Node Deletion: If the node to be deleted is the head node, the head pointer of the list must be updated accordingly.
  • Empty List: If the list is empty (head == NULL), no operation should proceed.

What is the algorithm to delete a node before a specific node?

Here is the step-by-step algorithm:

  • Traverse to the Target Node: Start from the head and traverse the list to find the node with the given key.
  • Check for Edge Cases: If the target node is NULL or its prev pointer is NULL, terminate the operation.
  • Identify the Node to Delete: The node to delete is curr->prev.
  • Update Pointers: Adjust the prev pointer of the target node and the next pointer of the preceding node (if it exists).
  • Free the Node: Deallocate the memory of the node to delete using free() to prevent memory leaks.

Can this algorithm be implemented in other programming languages besides C?

Yes, the algorithm can be implemented in other programming languages such as C++, Java, Python, and more. Here’s how:

  • C++: You can use classes to represent nodes and manage pointers.
  • Python: Leverage its dynamic typing and use objects to create a doubly linked list.
  • Java: Utilize classes and references to manage the next and prev pointers.

The logic remains the same, but syntax and memory management (like manual freeing in C) will differ.

How does the provided C code handle memory deallocation?

In C programming, memory for nodes is allocated dynamically using the malloc() function. When a node is deleted, the free() function is called to release the memory allocated to it. This ensures that:

  • The program does not cause memory leaks.
  • The deallocated memory can be reused by the system for other processes.

Proper memory management is crucial in C as it does not have automatic garbage collection like Java or Python.

Can the deletion operation fail, and how should it be handled?

Yes, the deletion operation can fail in the following scenarios:

  • Target Node Not Found: If the node with the specified key is not in the list, the function should simply return the unchanged head.
  • No Node to Delete: If the prev pointer of the target node is NULL, no operation is performed.

In both cases, it is critical to return the original head pointer to indicate that the list remains unchanged.

What is the time complexity of the deletion operation?

The time complexity of this operation is O(n), where n is the number of nodes in the list.

  • Reason: The algorithm traverses the list to find the node with the given key. This traversal takes linear time in the worst case (when the node is at the end of the list).
  • The actual deletion and pointer adjustment steps occur in constant time O(1).

Thus, the overall complexity is O(n).

How is the head node updated during the deletion process?

If the node to be deleted is the head node, the algorithm ensures that:

  • The head pointer is updated to point to the next node (if it exists).
  • The prev pointer of the new head node is set to NULL.

This ensures the list remains valid even after the head node is removed.

How can this approach be optimized for larger datasets?

For larger datasets, consider the following optimizations:

  • Use Additional Metadata: Store the size of the list or maintain direct references to nodes to reduce traversal time.
  • Indexing: Create an indexing mechanism to access nodes more efficiently.
  • Tailored Data Structures: Use advanced data structures like skip lists or trees if the list is part of a more extensive system.
  • Memory Pools: Manage memory more efficiently by reusing freed memory instead of calling malloc() and free() repeatedly.
Share.
Examsmeta Logo

Examsmeta serves as a comprehensive hub for educational resources across diverse disciplines. Designed to deliver high-quality, topic-wise notes and articles, it caters to students, educators, researchers, and lifelong learners. The goal is to make learning accessible, engaging, and effective for all. With a focus on providing detailed, accurate, and up-to-date content, Examsmeta fosters a passion for learning and supports both academic and professional growth. Whether it's exam preparation, research, or knowledge expansion, this platform offers guidance every step of the way.