In the field of computer science, evaluating how efficiently an algorithm performs as input size grows is crucial for optimizing applications. Asymptotic notations are an essential tool used to express an algorithm’s time or space complexity. Among these, Big-Omega (Ω) Notation plays a significant role in analyzing the best-case scenario for an algorithm.
In this detailed guide, we will explore Big-Omega (Ω) Notation thoroughly, delving into its definition, interpretation, and practical usage with code examples. We’ll also explain how to determine the asymptotic lower bound for various algorithms and break down the essential steps of understanding an algorithm’s best-case time complexity.
Table of Contents
What is Big-Omega (Ω) Notation?
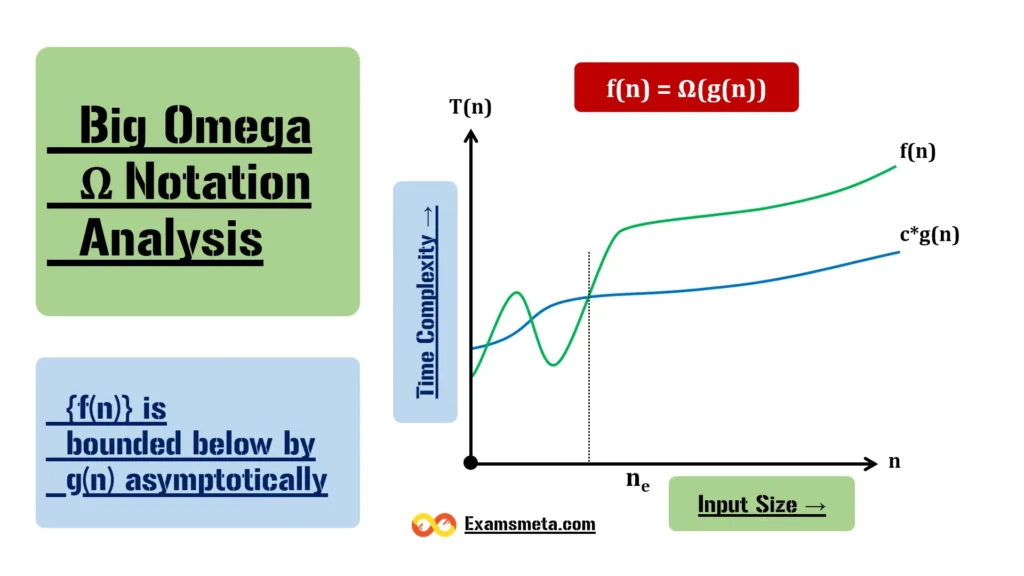
Big-Omega (Ω) Notation is an asymptotic notation that defines the lower bound for the growth rate of an algorithm’s time or space complexity. In simpler terms, it is used to represent the best-case scenario of an algorithm. If an algorithm’s time complexity is denoted as Ω(f(n)), it means that in the best possible situation, the algorithm will take at least f(n) steps, where n is the size of the input.
For example, an algorithm with a time complexity of Ω(n) will always take at least n steps to solve a problem as the input size grows, regardless of other factors.
It is important to note that Big-Omega (Ω) notation doesn’t provide an upper bound (the worst-case time complexity); rather, it guarantees that the algorithm will not execute in fewer than f(n) steps. Hence, it is less commonly used compared to other notations like Big-O (O) (which gives the upper bound) but is crucial in specific scenarios.
Formal Definition of Big-Omega (Ω) Notation
To define Big-Omega (Ω) rigorously, let’s look at the mathematical definition:
Given two functions f(n) and g(n), we say that:
$$ f(n) = Ω(g(n)) $$
if there exist positive constants c > 0 and n₀ ≥ 0 such that:
$$ f(n) ≥ c \cdot g(n) \text{ for all } n ≥ n₀ $$
In simpler terms, the function f(n) grows at least as fast as g(n), multiplied by a constant factor, when n becomes sufficiently large (larger than n₀). This provides a lower limit for the time complexity, ensuring that f(n) is never smaller than g(n) for large values of n.
Steps to Determine Big-Omega (Ω) Notation
To determine the Big-Omega (Ω) of an algorithm, follow these steps:
1. Break the Algorithm into Segments
First, break down the algorithm into smaller parts, focusing on individual loops, conditional statements, and recursive calls. Each part will have its own time complexity, and understanding each segment is crucial to figuring out the overall complexity.
2. Analyze Each Segment for the Best Case
Now, analyze each segment by counting the number of operations performed in the best-case scenario. For example, in some cases, loops may terminate early, or certain conditional branches might not be taken.
3. Summing Up the Time Complexities
Once you’ve evaluated each segment, combine their complexities. Usually, this involves summing up the complexities of different sections of code. Let’s assume that the resulting time complexity is f(n).
4. Eliminate Constants and Focus on the Lower Bound
Remove constant factors that don’t significantly affect the growth rate as n becomes large. Then, isolate the term that grows the fastest but still remains smaller than or equal to f(n) as n approaches infinity.
For example, if f(n) = 3n² + 5n + 2, the term n² dominates the growth, and other terms become negligible in comparison. Therefore, you can safely express the time complexity as Ω(n²).
Practical Example of Big-Omega (Ω) Notation
Let’s take a practical example where we aim to print all the possible pairs from an array. Consider the following C++ code:
#include <iostream>
using namespace std;
// Function to print all possible pairs in an array
int print(int a[], int n)
{
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j)
cout << a[i] << " " << a[j] << "\n";
}
}
return 0;
}
// Driver Code
int main()
{
int a[] = { 1, 2, 3 };
int n = sizeof(a) / sizeof(a[0]);
// Function call
print(a, n);
return 0;
}Step-by-Step Breakdown:
- Array Declaration and Size Calculation:
- An array a[] is declared with 3 elements: {1, 2, 3}.
- The size n of the array is calculated using the formula:
- $$ n = \frac{ \text{sizeof(a)} }{ \text{sizeof(a[0])} } $$
- In this case, n = 3.
- Nested Loops:
- The first loop runs n times, and for each iteration, the second loop runs n times. Together, these loops form a nested structure.
- For each pair (i, j) where i ≠ j, the code prints the elements a[i] and a[j].
Time Complexity:
The inner loop executes n times for each iteration of the outer loop, resulting in n² total operations. However, since there is a conditional check (i ≠ j), the number of actual print statements executed is n(n – 1). But for large input sizes, the conditional check has a minimal impact, and the algorithm’s best-case complexity can be approximated as Ω(n²).
Thus, the Big-Omega (Ω) time complexity for this algorithm is Ω(n²), meaning that the algorithm takes at least n² operations in the best-case scenario.
When to Use Big-Omega (Ω) Notation?
While Big-Omega (Ω) notation is less commonly used than other asymptotic notations like Big-O (O) or Theta (Θ), it is still valuable in certain cases:
- Best-Case Scenario:
- When you want to express the lower bound of an algorithm’s performance, for instance, for binary search, the best-case time complexity is Ω(1), as the target element may be found in the first comparison.
- Analyzing Lower Bound for Algorithm Optimization:
- Knowing the Ω complexity can help in determining the minimal runtime for an algorithm. This is useful for understanding the limits of how much an algorithm can be optimized.
Additional Examples and Applications of Big-Omega (Ω)
1. Binary Search
The binary search algorithm divides the search space in half at each step, resulting in a worst-case time complexity of O(log n). However, the best case occurs when the element to be found is located at the middle of the array during the first iteration. Therefore, the best-case complexity is:
$$ Ω(1) $$
This implies that binary search can take a constant amount of time in its best case, though the average and worst cases are much higher.
2. Linear Search
In a linear search, the algorithm traverses through all the elements to find a target value. The best-case scenario happens when the target element is found in the first position, resulting in a complexity of:
$$ Ω(1) $$
But in the worst-case scenario, it would need to traverse the entire array, yielding a complexity of O(n).
Conclusion
In conclusion, Big-Omega (Ω) notation is a critical tool for expressing the lower bound of an algorithm’s time or space complexity. Although it is less frequently used compared to Big-O (O) notation, understanding Ω is essential for analyzing the best-case performance of algorithms and determining their minimal time complexity. By mastering Big-Omega (Ω), you gain a deeper understanding of how algorithms behave, particularly in favorable conditions.
In programming, having knowledge of asymptotic notations such as Big-Omega (Ω), Big-O (O), and Theta (Θ) allows you to make well-informed decisions when designing and optimizing algorithms for various applications.
Example of Big-Omega (Ω) Notation in Programming Languages with Code Implementation
To understand Big-Omega (Ω) Notation better, let’s walk through an in-depth example using multiple programming languages like C++, C, Python, and Java. We will analyze the best-case time complexity of an algorithm designed to print all the possible pairs in an array. The goal is to evaluate the lower bound of the algorithm’s time complexity and implement the solution in different languages.
We’ll explain each step of coding specifically before the actual implementation, and we will also explore the Big-Omega (Ω) time complexity calculation for these implementations.
Algorithm Overview:
We will write a function that prints all possible pairs from an array of size n, but only if the two elements are not the same (i.e., i ≠ j). The nested loop structure ensures that the number of operations grows quadratically with the size of the input array.
Steps to Consider Before Coding:
- Array Initialization:
- In every language, initialize an array with a few elements (for demonstration purposes, we use an array of size 3).
- For different languages, the syntax to declare and initialize arrays will vary.
- Nested Loops:
- We will use two loops to iterate through the array.
- The outer loop will pick one element, and the inner loop will pair it with every other element in the array.
- A conditional check ensures that i ≠ j, so we don’t print the same element twice in the same pair.
- Output:
- Each time the conditional check succeeds, the elements will be printed as a pair.
- The total number of iterations of the inner loop gives us the time complexity.
- Time Complexity:
- The time complexity for this algorithm is quadratic in both the best and worst cases. We expect the best-case time complexity to be Ω(n²) because the algorithm will always take at least n² operations to print the pairs.
Let’s move forward with the implementation in different languages.
C++ Implementation
Step-by-Step Breakdown (C++):
- Array Declaration:
- Declare an array of integers.
- Compute its size using the formula
sizeof(a)/sizeof(a[0]).
- Nested Loops:
- The outer loop runs from 0 to
n-1. - The inner loop also runs from 0 to
n-1, printing pairs only when i ≠ j.
- The outer loop runs from 0 to
- Output:
- For each valid pair, print the elements.
C++ Code:
#include <iostream>
using namespace std;
// Function to print all possible pairs from an array
void printPairs(int arr[], int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j) {
cout << arr[i] << " " << arr[j] << endl;
}
}
}
}
int main() {
// Declare and initialize the array
int arr[] = {1, 2, 3};
int n = sizeof(arr) / sizeof(arr[0]);
// Call the function to print pairs
printPairs(arr, n);
return 0;
}Output:
1 2
1 3
2 1
2 3
3 1
3 2Big-Omega (Ω) Analysis:
- Best-Case Time Complexity: The nested loops run n² times. Therefore, the best-case time complexity is Ω(n²).
- The algorithm must run the inner loop for every element in the outer loop, making it a minimum of n² iterations.
2. C Implementation
Step-by-Step Breakdown (C):
- Array Initialization:
- In C, use an integer array and calculate its size using
sizeofoperator.
- In C, use an integer array and calculate its size using
- Nested Loops:
- Similar to C++, use two loops to print pairs of elements where i ≠ j.
C Code:
#include <stdio.h>
// Function to print all possible pairs from an array
void printPairs(int arr[], int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j) {
printf("%d %d\n", arr[i], arr[j]);
}
}
}
}
int main() {
// Declare and initialize the array
int arr[] = {1, 2, 3};
int n = sizeof(arr) / sizeof(arr[0]);
// Call the function to print pairs
printPairs(arr, n);
return 0;
}Output:
1 2
1 3
2 1
2 3
3 1
3 2Big-Omega (Ω) Analysis:
- Best-Case Time Complexity: Ω(n²) as it requires n² operations to print all pairs, even in the best case.
3. Python Implementation
Step-by-Step Breakdown (Python):
- Array Declaration:
- In Python, declare an array using a list.
- Nested Loops:
- Use Python’s for-loop to iterate through the list and print the valid pairs.
- Output:
- The
print()function will output each pair of numbers.
- The
Python Code:
# Function to print all possible pairs from a list
def print_pairs(arr):
n = len(arr)
for i in range(n):
for j in range(n):
if i != j:
print(arr[i], arr[j])
# Declare and initialize the array
arr = [1, 2, 3]
# Call the function to print pairs
print_pairs(arr)Output:
1 2
1 3
2 1
2 3
3 1
3 2Big-Omega (Ω) Analysis:
- Best-Case Time Complexity: Ω(n²) for the same reasons as C++ and C implementations. The nested loops will always require n² operations.
4. Java Implementation
Step-by-Step Breakdown (Java):
- Array Initialization:
- In Java, initialize an array of integers using the
newkeyword.
- In Java, initialize an array of integers using the
- Nested Loops:
- Implement two
forloops to iterate through the array and print pairs when i ≠ j.
- Implement two
- Output:
- Use
System.out.println()to output the pairs.
- Use
Java Code:
public class Main {
// Function to print all possible pairs from an array
public static void printPairs(int[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j) {
System.out.println(arr[i] + " " + arr[j]);
}
}
}
}
public static void main(String[] args) {
// Declare and initialize the array
int[] arr = {1, 2, 3};
// Call the function to print pairs
printPairs(arr);
}
}Output:
1 2
1 3
2 1
2 3
3 1
3 2Big-Omega (Ω) Analysis:
- Best-Case Time Complexity: Ω(n²), just like in the other languages. The inner loop executes n times for each of the n iterations of the outer loop.
The code implementations in C++, C, Python, and Java demonstrate the usage of nested loops to print all pairs from an array. In each case, the best-case time complexity is Ω(n²) because the algorithm requires at least n² operations to complete the task, regardless of the input. This is a common characteristic of algorithms involving nested loops.
Understanding the Big-Omega (Ω) Notation helps in evaluating the minimum time required by an algorithm, which is an important aspect of performance analysis, especially when trying to assess the lower bound of execution time.
Informative Table Based on Big-Omega (Ω) Notation
Here’s an informative table summarizing the key aspects of Big-Omega (Ω) Notation in the context of algorithm analysis:
| Aspect | Description |
|---|---|
| Definition | Big-Omega (Ω) notation represents the asymptotic lower bound of an algorithm’s time or space complexity. It provides a guarantee that the algorithm will take at least this much time for sufficiently large input sizes. |
| Mathematical Definition | A function f(n) = Ω(g(n)) if there exist constants c > 0 and n₀ ≥ 0 such that f(n) ≥ c * g(n) for all n ≥ n₀. |
| Purpose | It describes the best-case scenario or minimum time complexity for an algorithm. It is used when analyzing how fast an algorithm can run in the most favorable conditions. |
| Symbols | – f(n): Actual running time of the algorithm based on input size n – g(n): Growth function representing the minimum performance bound |
| Usage | To find the lower bounds of an algorithm’s performance, or how fast it can potentially run in the best case. |
| Relation to Other Notations | – Big-O (O): Describes the upper bound (worst-case) – Big-Theta (Θ): Describes the tight bound (both upper and lower) |
| Examples of Big-Omega | – Ω(1): Constant time, meaning the algorithm will always take at least a fixed amount of time – Ω(log n): Logarithmic time, such as binary search in the best case |
| Steps to Determine Big-Omega | 1. Break down the algorithm into segments. 2. Find the time complexity of each segment under best-case conditions. 3. Simplify and remove constants. 4. Express the result as Ω(g(n)). |
| Typical Algorithms | – Linear Search: Best-case time complexity is Ω(1) when the target element is the first in the list. – Binary Search: Best-case time complexity is Ω(1). |
| Real-World Relevance | Big-Omega helps understand the fastest possible runtime of algorithms, which is important when aiming for optimal performance and when evaluating the efficiency of specific algorithms. |
| Advantages | – Provides insights into how an algorithm performs under the most favorable conditions. – Helps in identifying the lower performance bound for optimization purposes. |
| Limitations | – Big-Omega (Ω) doesn’t provide information about the upper bounds or how the algorithm behaves in the average or worst cases. – Not frequently used compared to Big-O (O). |
| Comparison with Big-O | Big-O (O) tells us how slow the algorithm can potentially get, while Big-Omega (Ω) tells us how fast it can potentially be. |
| Best-Case Scenario | Big-Omega shows the best-case time complexity, such as Ω(1) for a linear search when the first element is the target, or Ω(log n) for algorithms like binary search. |
This table highlights the essential details of Big-Omega (Ω) notation, providing a clear reference for understanding its significance and application in algorithm analysis.
Related Articles
- Understanding Big-Theta (Θ) Notation in Algorithm Analysis
- Big-Omega (Ω) Notation in Algorithm Analysis: A Comprehensive Guide
- Big O Notation Tutorial – A Comprehensive Guide to Algorithm Complexity Analysis
- Asymptotic Notation and Complexity Analysis of Algorithms
- Understanding Algorithms in Computer Science: A Comprehensive Guide
- Understanding Trie Data Structure in Depth: A Comprehensive Guide
- Real-Life Example of the Brute Force Algorithm: Password Cracking
- Brute Force Algorithm: Comprehensive Exploration, Pros, Cons, & Applications
- Analyzing an Algorithm and its Complexity: A Comprehensive Guide
- Understanding Algorithms: A Comprehensive Introduction
- Understanding Hashing: The Key to Fast and Efficient Data Storage and Retrieval
- Hierarchical Data Structures: Binary Trees, Binary Search Trees, Heaps, & Hashing
- Comprehensive Overview on Applications of Arrays, Advantages & Disadvantages of Arrays
- Matrix Data Structure: A Comprehensive Guide to the Two-Dimensional Array
- Introduction to Array Data Structures: A Comprehensive Guide
- Understanding Linear Data Structures: A Comprehensive Exploration
- Difference Between Linear & Non-Linear Data Structures: A Comprehensive Overview
- Tree Data Structures: Definitions, Types, Applications, & Comprehensive Exploration
- Cyclic Graphs: Structure, Applications, Advantages, & Challenges in Data Structures
- Introduction to Directed Acyclic Graph (DAG): A Comprehensive Exploration with Examples
- Strongly, Unilaterally, and Weakly Connected Graphs in Data Structures
- Unweighted Graphs: Definition, Applications, Advantages, and Disadvantages
- Comprehensive Guide to Adjacency Lists in Data Structures
- Adjacency Matrix: A Comprehensive Guide to Graph Representation
- Understanding Weighted Graphs: A Comprehensive Exploration
- Understanding Undirected Graphs: Structure, Applications, and Advantages
- Understanding Directed Graphs: Characteristics, Applications, & Real-World Examples
- Graph Data Structure in Computer Science: A Comprehensive Exploration
- Understanding Data Structures: An In-Depth Exploration
- A Comprehensive Guide to DSA: Data Structures and Algorithms
Read More Articles
- Data Structure (DS) Array:
- Why the Analysis of Algorithms is Important?
- Worst, Average, and Best Case Analysis of Algorithms: A Comprehensive Guide
- Understanding Pointers in C Programming: A Comprehensive Guide
- Understanding Arrays in Data Structures: A Comprehensive Exploration
- Memory Allocation of an Array: An In-Depth Comprehensive Exploration
- Understanding Basic Operations in Arrays: A Comprehensive Guide
- Understanding 2D Arrays in Programming: A Comprehensive Guide
- Mapping a 2D Array to a 1D Array: A Comprehensive Exploration
- Data Structure Linked List:
- Understanding Linked Lists in Data Structures: A Comprehensive Exploration
- Types of Linked List: Detailed Exploration, Representations, and Implementations
- Understanding Singly Linked Lists: A Detailed Exploration
- Understanding Doubly Linked List: A Comprehensive Guide
- Operations of Doubly Linked List with Implementation: A Detailed Exploration
- Insertion in Doubly Linked List with Implementation: A Detailed Exploration
- Inserting a Node at the beginning of a Doubly Linked List: A Detailed Exploration
- Inserting a Node After a Given Node in a Doubly Linked List: A Detailed Exploration
- Inserting a Node Before a Given Node in a Doubly Linked List: A Detailed Exploration
- Inserting a Node at a Specific Position in a Doubly Linked List: A Detailed Exploration
- Inserting a New Node at the End of a Doubly Linked List: A Detailed Exploration
- Deletion in a Doubly Linked List with Implementation: A Comprehensive Guide
- Deletion at the Beginning in a Doubly Linked List: A Detailed Exploration
- Deletion after a given node in Doubly Linked List: A Comprehensive Guide
- Deleting a Node Before a Given Node in a Doubly Linked List: A Detailed Exploration
- Deletion at a Specific Position in a Doubly Linked List: A Detailed Exploration
- Deletion at the End in Doubly Linked List: A Comprehensive Exploration
- Introduction to Circular Linked Lists: A Comprehensive Guide
- Understanding Circular Singly Linked Lists: A Comprehensive Guide
- Circular Doubly Linked List: A Comprehensive Guide
- Insertion in Circular Singly Linked List: A Comprehensive Guide
- Insertion in an Empty Circular Linked List: A Detailed Exploration
- Insertion at the Beginning in Circular Linked List: A Detailed Exploration
- Insertion at the End of a Circular Linked List: A Comprehensive Guide
- Insertion at a Specific Position in a Circular Linked List: A Detailed Exploration
- Deletion from a Circular Linked List: A Comprehensive Guide
- Deletion from the Beginning of a Circular Linked List: A Detailed Exploration
- Deletion at Specific Position in Circular Linked List: A Detailed Exploration
- Deletion at the End of a Circular Linked List: A Comprehensive Guide
- Searching in a Circular Linked List: A Comprehensive Exploration
Frequently Asked Questions (FAQs)
What is the purpose of asymptotic notations in the analysis of algorithms?
Asymptotic notations are used to describe the performance of algorithms in terms of time or space as the input size grows. These notations provide a way to compare algorithms by abstracting away constant factors and focusing on the growth rate. In algorithm analysis, the goal is to understand how an algorithm performs as the input size approaches infinity. This helps identify the efficiency of the algorithm, independent of the system’s hardware or compiler optimizations.
Asymptotic notations include:
- Big-O (O) for the upper bound (worst-case scenario)
- Big-Omega (Ω) for the lower bound (best-case scenario)
- Big-Theta (Θ) for tight bounds (both upper and lower)
By using these notations, we can classify algorithms based on their scalability and ensure that we choose the most efficient algorithm for large inputs.
What is Big-Omega (Ω) Notation, and why is it important?
Big-Omega (Ω) Notation is used to define the asymptotic lower bound of an algorithm’s time complexity. It describes the best-case performance scenario, giving a lower limit on how quickly an algorithm can complete a task as the input size increases. Formally, a function f(n) is Ω(g(n)) if there exist constants c > 0 and n₀ ≥ 0 such that f(n) ≥ c * g(n) for all n ≥ n₀.
In simpler terms, Big-Omega gives a guarantee that the algorithm will take at least a certain amount of time, no matter what. It’s important because it provides insight into the fastest possible execution time for an algorithm, which can be useful for optimization. For example, if an algorithm has Ω(n²) time complexity, we know that even in the best case, it will take at least n² operations, so any further optimization should target reducing this bound.
How does Big-Omega (Ω) differ from Big-O (O) Notation?
While both Big-O (O) and Big-Omega (Ω) notations are used to describe the performance of algorithms, they refer to different aspects of time complexity:
- Big-O (O) Notation: It defines the upper bound or worst-case time complexity of an algorithm. It answers the question: What is the maximum time or space an algorithm will take?
- Big-Omega (Ω) Notation: It defines the lower bound or best-case time complexity of an algorithm. It answers the question: What is the minimum time or space required by the algorithm?
In essence, Big-O deals with how slow the algorithm can potentially get, while Big-Omega deals with how fast it can be.
Can you explain the formal definition of Big-Omega (Ω) Notation?
Yes, the formal definition of Big-Omega (Ω) Notation is as follows:
Given two functions f(n) and g(n), we say that f(n) = Ω(g(n)) if there exist constants c > 0 and n₀ ≥ 0 such that:
f(n) ≥ c * g(n) for all n ≥ n₀.
This means that beyond a certain point (denoted by n₀), the function f(n) will always grow at least as fast as g(n) when multiplied by the constant c. This formalization helps in determining the lower limit for an algorithm’s execution time.
For example, if we say f(n) = Ω(n), it implies that beyond a certain input size, f(n) will grow at least linearly with n.
What are some real-world examples where Big-Omega (Ω) Notation is used?
In real-world applications, Big-Omega (Ω) Notation is useful in scenarios where we are interested in the best-case scenario of an algorithm’s performance:
- Sorting Algorithms: For algorithms like QuickSort, the best-case time complexity is Ω(n log n), which occurs when the pivot element always splits the array into two roughly equal halves.
- Searching Algorithms: In the case of binary search, the best-case time complexity is Ω(1), which occurs when the target element happens to be the middle element of the array on the first comparison.
- Graph Algorithms: For algorithms like Dijkstra’s algorithm, the best-case scenario occurs when the graph has no negative weights, making it easier to find the shortest path in Ω(E + V log V) time.
- Hash Table Operations: In the best-case scenario, operations like insertion, deletion, and lookup in a hash table can be performed in Ω(1) time.
How do you determine Big-Omega (Ω) Notation for a given algorithm?
To determine the Big-Omega (Ω) notation for an algorithm, follow these steps:
- Break down the algorithm into smaller components and understand each component’s runtime in terms of n (input size).
- Find the complexity of each segment assuming that the algorithm takes the least amount of time (best-case scenario). This means analyzing the algorithm when the input is ideal.
- Combine the complexities of all the segments to create a function f(n) that represents the total number of operations in the best case.
- Remove constants and lower-order terms. Choose the term with the slowest growth rate compared to the rest and consider it the lower bound function g(n).
- Finally, express the algorithm’s best-case time complexity as Ω(g(n)).
For example, if an algorithm has a best-case scenario that requires n² operations, the best-case time complexity will be Ω(n²).
What is the importance of lower bounds (Big-Omega) in algorithm design?
Lower bounds, represented by Big-Omega (Ω) Notation, are crucial in algorithm design because they provide insight into how much faster an algorithm can potentially run. Knowing the lower bound allows computer scientists to understand the limits of optimization for an algorithm.
- Insight into Performance Limits: By determining the best-case time complexity, developers can avoid spending effort on trying to improve an algorithm that has already reached its theoretical performance limits.
- Algorithm Comparison: Lower bounds are particularly useful when comparing algorithms. For instance, if one algorithm has Ω(n log n) and another has Ω(n²), the first algorithm is generally better in practice for large inputs, even though they might have similar worst-case time complexities.
- Benchmarking: Lower bounds give a reference point to assess how close a given algorithm’s performance is to optimal in the best-case scenario.
Can you give an example of how Big-Omega (Ω) Notation works with a simple algorithm?
Consider an algorithm to find the maximum number in an unsorted array:
int findMax(int arr[], int n) {
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return max;
}Steps to Analyze the Algorithm:
- Initialization: The algorithm initializes the variable max to the first element of the array. This step takes O(1) time.
- Loop Iteration: The algorithm then iterates through the array from index 1 to n-1, performing n-1 comparisons.
- Best-Case Scenario: In the best case, the first element of the array is the maximum, so no updates are made to max. Still, the algorithm must compare every element, meaning that the best-case scenario still requires n-1 comparisons.
Thus, the Big-Omega (Ω) time complexity is Ω(n) since the algorithm must always make at least n-1 comparisons.
Why is Big-Omega (Ω) notation less commonly used than Big-O (O)?
While Big-Omega (Ω) notation is important for understanding the best-case performance of an algorithm, it is less commonly used than Big-O (O) notation for several reasons:
- Worst-Case Performance is More Critical: In real-world applications, the worst-case scenario is often more important than the best case. Users want to know how slow an algorithm can potentially be to make decisions about whether it’s suitable for their needs.
- Optimization Focuses on Worst-Case: Most of the time, developers aim to optimize algorithms to handle the worst-case scenario because that is when systems may experience bottlenecks.
- Best Case is Less Predictive: Knowing the best-case time complexity doesn’t always give much practical insight into the algorithm’s overall efficiency, as the best case might be rare or unrealistic for most input sets.
Can an algorithm have different Big-Omega (Ω) notations for different input cases?
Yes, an algorithm can have multiple Big-Omega (Ω) notations, depending on different input scenarios. For example, in a **binary search
algorithm**, the best-case time complexity is *Ω(1)* when the target element happens to be the middle element. However, in the worst case (or when we focus on best-case complexity across different sections of the input), the time complexity could be Ω(log n) if the input is structured in a way that necessitates several comparisons.
Thus, the best-case complexity might vary based on specific input characteristics, leading to multiple Big-Omega expressions.
Can Big-Omega (Ω) and Big-O (O) for an algorithm be the same?
Yes, Big-Omega (Ω) and Big-O (O) for an algorithm can be the same when the algorithm’s best-case and worst-case complexities are identical. This happens when the algorithm’s performance doesn’t vary with different inputs and consistently runs within the same time limits.
An example is Merge Sort, which has a time complexity of O(n log n) and Ω(n log n). Whether the input is already sorted, reverse sorted, or randomly arranged, the algorithm always performs the same number of operations because it always divides the array and merges it back in a systematic way. In such cases, the time complexity is also described by Big-Theta (Θ) notation.
What is the relationship between Big-O (O), Big-Omega (Ω), and Big-Theta (Θ)?
The three notations are closely related:
- Big-O (O): Describes the upper bound or worst-case scenario of an algorithm. It tells us the maximum time or space an algorithm will take as input size grows.
- Big-Omega (Ω): Describes the lower bound or best-case scenario of an algorithm. It tells us the minimum time or space an algorithm will take for certain inputs.
- Big-Theta (Θ): Describes the tight bound of an algorithm, where the algorithm’s growth rate is the same in both the best and worst cases. When f(n) = Θ(g(n)), it means that the algorithm’s time complexity is sandwiched between the lower and upper bounds provided by Big-Omega and Big-O.
For example, Merge Sort has Θ(n log n) complexity because its best, worst, and average cases are all in the same order.
How does Big-Omega (Ω) apply to space complexity analysis?
Just like with time complexity, Big-Omega (Ω) can also be used to describe the best-case space complexity of an algorithm. Space complexity refers to the amount of memory an algorithm needs relative to the input size.
For example, consider a recursive algorithm like Fibonacci:
def fibonacci(n):
if n == 0 or n == 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)In the best-case scenario, when the input is n = 0, the algorithm uses Ω(1) space since it doesn’t need to recurse. However, for larger inputs, the space complexity increases because of the recursive call stack.
Thus, Big-Omega (Ω) helps in understanding how little memory an algorithm could use at a minimum.
What is the significance of Big-Omega (Ω) Notation in parallel computing?
In parallel computing, Big-Omega (Ω) notation becomes particularly important in determining the minimum amount of work required to complete a task, even when multiple processors are used. Understanding the lower bound in such scenarios helps in predicting the best possible performance and determining if adding more resources (like processors) will result in a performance gain.
For example, consider an algorithm that requires n² operations. Even if we parallelize it across p processors, we may not reduce the time complexity below Ω(n/p) due to limitations in how the problem can be divided. This lower bound is critical for designing efficient parallel algorithms, as it tells us how far we can go in optimizing.
Can Big-Omega (Ω) Notation be used for probabilistic algorithms?
Yes, Big-Omega (Ω) notation can be used for probabilistic or randomized algorithms, but it’s often applied to the expected best-case scenario. In probabilistic algorithms, the time complexity may depend on the probability distribution of inputs or random choices made by the algorithm itself.
For example, in Randomized QuickSort, the best-case time complexity (when the pivot divides the array into perfectly equal halves) is Ω(n log n). However, since the pivot selection is random, the expected time complexity is O(n log n), but the best-case scenario occurs less frequently.
In such cases, Big-Omega helps to describe the minimum amount of time required, even considering randomness.

