When studying algorithms, one of the most important things to understand is how their performance scales with the size of the input. This is where Big O notation comes into play. Big O notation is a mathematical tool used in computer science to describe the efficiency of algorithms, particularly their time complexity and space complexity. This guide will walk you through the fundamentals of Big O notation, explain its significance, and provide examples to help you analyze the performance of algorithms.
Table of Contents
What is Big O Notation?
Big O notation, often referred to as the “Order of” an algorithm, is a way to represent the upper limit of an algorithm’s time complexity or space complexity. In simpler terms, it describes the worst-case scenario in terms of performance as the input size grows. When analyzing algorithms, we are usually interested in how they behave when dealing with very large inputs—this is where Big O notation becomes useful.
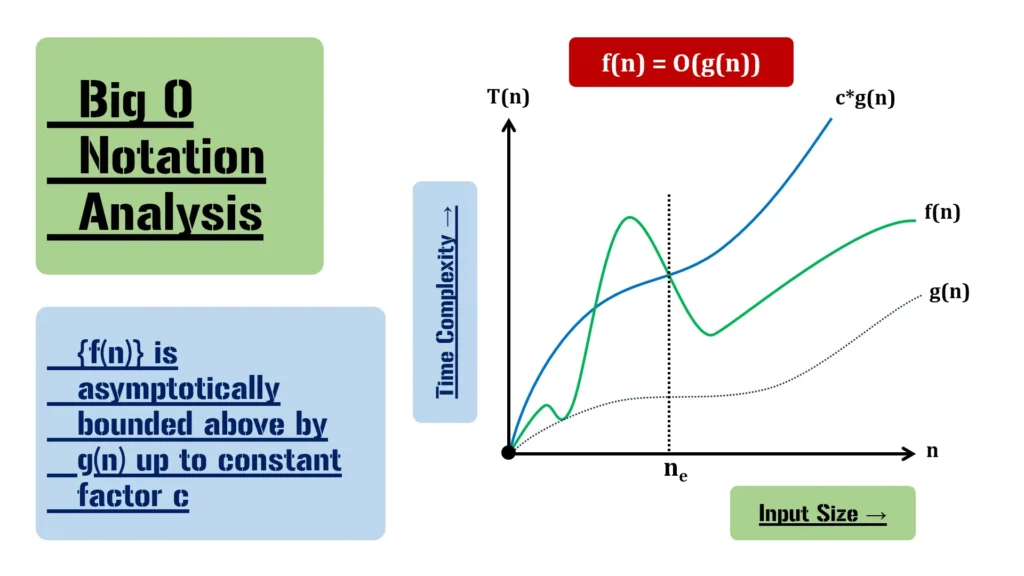
Definition of Big O Notation
Formally, given two functions f(n) and g(n), we say that f(n) = O(g(n)) if there exist constants c > 0 and n₀ ≥ 0 such that:
f(n) ≤ c * g(n) for all n ≥ n₀.
This means that f(n) grows at most as fast as g(n) multiplied by some constant c after a certain point n₀. In other words, Big O notation describes the upper bound of an algorithm’s growth rate.
Why is Big O Notation Important?
Big O notation is critical for multiple reasons:
- Algorithm Efficiency: It helps us analyze the efficiency of algorithms, allowing developers to understand how algorithms behave as input sizes grow. It provides a way to describe an algorithm’s time complexity (how fast it runs) and space complexity (how much memory it uses).
- Performance Comparison: It enables us to compare different algorithms or data structures and choose the most efficient one for a given problem.
- Scalability: By understanding the scalability of an algorithm, Big O notation allows us to predict how the algorithm will perform as the input size grows.
- Optimization: Knowing the Big O complexity helps in optimizing code, ensuring that programs run faster and use less memory.
Properties of Big O Notation
Understanding the properties of Big O notation is crucial when analyzing complex algorithms. Let’s break down the core properties:
1. Reflexivity
For any function f(n), we can say f(n) = O(f(n)). This simply means that a function is always Big O of itself.
Example: If f(n) = n², then f(n) = O(n²).
2. Transitivity
If f(n) = O(g(n)) and g(n) = O(h(n)), then f(n) = O(h(n)). This property is helpful when breaking down more complex algorithms into smaller parts.
Example: If f(n) = n³, g(n) = n², and h(n) = n⁴, then f(n) = O(g(n)), g(n) = O(h(n)), and hence f(n) = O(h(n)).
3. Constant Factor Rule
If f(n) = O(g(n)), then multiplying f(n) by any constant c > 0 does not change its Big O classification.
Example: If f(n) = n and g(n) = n², then f(n) = O(g(n)). Multiplying f(n) by 2 (or any constant) still yields O(g(n)).
4. Sum Rule
If f(n) = O(g(n)) and h(n) = O(g(n)), then f(n) + h(n) = O(g(n)). This property is useful when analyzing algorithms with multiple parts that contribute to the overall complexity.
Example: If f(n) = n², g(n) = n³, and h(n) = n⁴, then f(n) = O(g(n)) and h(n) = O(g(n)). Therefore, f(n) + h(n) = O(g(n)).
5. Product Rule
If f(n) = O(g(n)) and h(n) = O(k(n)), then f(n) * h(n) = O(g(n) * k(n)).
Example: If f(n) = n, g(n) = n², h(n) = n³, and k(n) = n⁴, then f(n) = O(g(n)) and h(n) = O(k(n)). Hence, f(n) * h(n) = O(n⁵).
6. Composition Rule
If f(n) = O(g(n)) and g(n) = O(h(n)), then f(g(n)) = O(h(n)).
Example: If f(n) = n², g(n) = n, and h(n) = n³, then f(n) = O(g(n)) and g(n) = O(h(n)). Hence, f(g(n)) = O(h(n)) = O(n³).
Common Big O Notations
Let’s now explore the most common Big O notations used in algorithm analysis:
1. O(1) – Constant Time Complexity
An algorithm is said to have constant time complexity if its running time does not depend on the input size n. No matter how large n becomes, the algorithm always takes the same amount of time to complete.
Example: Accessing a specific element in an array by index has O(1) time complexity because the operation always takes the same amount of time, regardless of the array’s size.
int getElement(int arr[], int index) {
return arr[index]; // O(1)
}2. O(n) – Linear Time Complexity
An algorithm has O(n) time complexity if its running time grows linearly with the size of the input. For example, an algorithm that iterates through all elements in an array has O(n) complexity.
Example: Linear search through an array.
bool findElement(int arr[], int n, int key) {
for (int i = 0; i < n; i++) {
if (arr[i] == key) {
return true; // O(n)
}
}
return false;
}3. O(log n) – Logarithmic Time Complexity
An algorithm has O(log n) time complexity if the running time increases logarithmically with the size of the input. This commonly occurs in algorithms that divide the input in half at each step.
Example: Binary search is a classic example of an algorithm with O(log n) complexity.
int binarySearch(int arr[], int l, int r, int x) {
if (r >= l) {
int mid = l + (r - l) / 2;
if (arr[mid] == x)
return mid;
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
return binarySearch(arr, mid + 1, r, x);
}
return -1; // O(log n)
}In binary search, the array is divided into two halves at each step, reducing the problem size from n to n/2.
4. O(n²) – Quadratic Time Complexity
Quadratic time complexity arises when an algorithm performs a linear operation n times for each element in a list. This often happens in algorithms that require comparing every element to every other element.
Example: Bubble sort has O(n²) complexity.
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
}
}
} // O(n²)
}The bubble sort algorithm performs n passes over an array of size n, making it inefficient for large inputs.
5. O(2ⁿ) – Exponential Time Complexity
Exponential time complexity means that the running time doubles with each addition to the input size. Algorithms with this complexity are often impractical for large inputs due to their extremely rapid growth.
Example: Generating all subsets of a set.
void generateSubsets(int arr[], int n) {
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
if (i & (1 << j)) {
cout << arr[j] << " ";
}
}
cout << endl;
} // O(2ⁿ)
}How to Determine Big O Notation?
When analyzing an algorithm’s complexity, you can follow these steps to determine its Big O notation:
1. Identify the Dominant Term
Examine the function and identify the term that grows the fastest as the input size increases. For example, if the function is f(n) = 3n³ + 2n² + 5n + 1, the dominant term is n³.
2. Ignore Constants and Lower-Order Terms
In Big O notation, we focus on the highest-order term and ignore constants. Thus, 3n³ simplifies to O(n³).
3. Write the Big O Notation
Finally, express the complexity in terms of Big O notation. In the example above, the complexity would be written as O(n³).
Big O Notation Through Practical Coding Examples
Understanding Big O notation through practical coding examples can help clarify how algorithm efficiency is measured across various programming languages. Below, is a detailed implementation of a common algorithm—Bubble Sort—in C++, C, Python, and Java.
Bubble Sort Overview
Bubble Sort is a straightforward sorting algorithm that repeatedly steps through the list to be sorted, compares adjacent elements, and swaps them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, indicating that the list is sorted.
Big O Analysis of Bubble Sort
- Best Case: O(n) — This occurs when the input list is already sorted.
- Average Case: O(n²) — The average time complexity for unsorted data.
- Worst Case: O(n²) — This occurs when the input list is sorted in reverse order.
The space complexity of Bubble Sort is O(1) because it only uses a constant amount of additional space for temporary variables.
1. C++ Implementation of Bubble Sort
#include <iostream>
using namespace std;
void bubbleSort(int arr[], int n) {
bool swapped;
// Loop through each element in the array
for (int i = 0; i < n - 1; i++) {
swapped = false; // Track if a swap was made in this pass
// Compare adjacent elements
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Swap if elements are in the wrong order
swap(arr[j], arr[j + 1]);
swapped = true; // Set swapped to true
}
}
// If no swaps were made, the array is sorted
if (!swapped) break;
}
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, n);
cout << "Sorted array: \n";
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}Explanation:
- Input: An array of integers to be sorted.
- Loop Structure: The outer loop runs through each element, and the inner loop compares adjacent elements.
- Swapping: If an element is greater than the next, it swaps them.
- Optimization: If no swaps occur in a pass, it breaks out of the loop, indicating that the array is sorted.
Output:
Sorted array:
11 12 22 25 34 64 902. C Implementation of Bubble Sort
#include <stdio.h>
void bubbleSort(int arr[], int n) {
int i, j, temp;
// Loop through each element in the array
for (i = 0; i < n - 1; i++) {
// Compare adjacent elements
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Swap if elements are in the wrong order
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, n);
printf("Sorted array: \n");
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}Explanation:
- The C implementation follows a similar logic as the C++ version.
- Uses
printffor output and simple integer swapping for elements.
Output:
Sorted array:
11 12 22 25 34 64 90 3. Python Implementation of Bubble Sort
def bubble_sort(arr):
n = len(arr)
# Loop through each element in the array
for i in range(n):
swapped = False # Track if a swap was made
# Compare adjacent elements
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
# Swap if elements are in the wrong order
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True # Set swapped to true
# If no swaps occurred, the array is sorted
if not swapped:
break
# Test the bubble sort implementation
arr = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(arr)
print("Sorted array:", arr)Explanation:
- Python uses a more concise syntax with tuple swapping for the elements.
- The logic is identical to that in C++ and C.
Output:
Sorted array: [11, 12, 22, 25, 34, 64, 90]4. Java Implementation of Bubble Sort
public class BubbleSort {
// Method to perform bubble sort
public static void bubbleSort(int arr[]) {
int n = arr.length;
// Loop through each element in the array
for (int i = 0; i < n - 1; i++) {
boolean swapped = false; // Track if a swap was made
// Compare adjacent elements
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Swap if elements are in the wrong order
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true; // Set swapped to true
}
}
// If no swaps occurred, the array is sorted
if (!swapped) break;
}
}
public static void main(String[] args) {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
bubbleSort(arr);
System.out.println("Sorted array: ");
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
}Explanation:
- The Java implementation follows the same logic with similar structure and syntax.
- Uses a boolean flag to determine if any swaps were made during a pass.
Output:
Sorted array:
11 12 22 25 34 64 90 Summary of the Implementations
- Each implementation of Bubble Sort across different programming languages adheres to the same basic logic and structure.
- The choice of language affects syntax but not the underlying algorithm.
- Bubble Sort serves as a clear example of how to analyze and implement an algorithm while considering its time complexity (O(n²) in the average and worst cases) and space complexity (O(1)).
Learning Outcomes
- Understand Big O Notation: Recognize how algorithm efficiency is measured.
- Cross-Language Implementation: Observe how the same algorithm is implemented in C++, C, Python, and Java.
- Performance Analysis: Appreciate how different inputs can affect the running time of algorithms, particularly for a simple sorting algorithm like Bubble Sort.
By practicing these implementations and analyzing their performance, you’ll gain valuable insights into algorithm efficiency and optimization strategies across different programming languages.
Conclusion
Understanding Big O notation is essential for anyone involved in algorithm design and analysis. It provides a systematic way to analyze and compare the performance of algorithms in terms of their time complexity and space complexity. Whether you are implementing simple sorting algorithms or working with more advanced graph traversal techniques, Big O notation equips you with the tools needed to assess scalability and efficiency.
Frequently Asked Questions (FAQs) About Big O Notation
Big O notation is an essential topic in computer science, particularly in the analysis of algorithms. To help you master this concept, we’ve compiled 15 detailed FAQs with comprehensive answers.
What is Big O Notation?
Big O notation is a mathematical representation used to describe the efficiency of an algorithm in terms of its time complexity and space complexity. It focuses on the worst-case scenario of how an algorithm’s performance scales as the size of the input data grows. In Big O notation, the complexity is expressed as a function of n, where n is the size of the input.
For example:
- O(n) describes linear time complexity, where the algorithm’s performance scales proportionally with the size of the input.
- O(1) describes constant time complexity, where the algorithm’s performance does not depend on the size of the input.
Why is Big O Notation Important?
Big O notation is crucial for several reasons:
- Predicting Performance: It helps predict how an algorithm will perform as the input size increases, which is important for designing scalable systems.
- Comparing Algorithms: Developers can compare the efficiency of different algorithms and choose the most optimal one for a given task. For example, O(log n) algorithms are generally more efficient than O(n²) algorithms for large inputs.
- Optimizing Code: By understanding the time and space complexity, developers can optimize their code to improve performance, especially in resource-intensive applications.
- Scalability: In large-scale systems, knowing the scalability of an algorithm ensures that applications perform efficiently under varying workloads.
What Are the Most Common Big O Notations?
Some common Big O notations used to describe the time complexity of algorithms are:
- O(1) – Constant Time Complexity: The algorithm runs at the same time regardless of the input size.
- Example: Accessing an element in an array by index.
- O(n) – Linear Time Complexity: The algorithm’s performance grows linearly with the size of the input.
- Example: Traversing an array or a linked list.
- O(log n) – Logarithmic Time Complexity: The algorithm reduces the problem size by a constant factor in each step.
- Example: Binary search.
- O(n²) – Quadratic Time Complexity: The algorithm’s performance grows quadratically with the input size.
- Example: Bubble sort.
- O(2ⁿ) – Exponential Time Complexity: The algorithm’s performance doubles with each addition to the input size.
- Example: Generating all subsets of a set.
- O(n!) – Factorial Time Complexity: The algorithm’s time complexity increases factorially with the size of the input.
- Example: Generating all permutations of a list.
What is Time Complexity and How is it Measured?
Time complexity is a way to represent the amount of time an algorithm takes to complete as a function of the input size n. It gives us an upper bound on the algorithm’s running time in the worst case. The time complexity is typically expressed in Big O notation, which focuses on the dominant term that grows the fastest as n increases.
For example:
- O(n) means the algorithm’s runtime grows linearly with the input size.
- O(n²) means the runtime grows quadratically as the input size increases.
Time complexity is measured by counting the number of operations the algorithm performs relative to the input size, ignoring constant factors.
What is Space Complexity?
Space complexity refers to the amount of memory an algorithm uses as a function of the input size. Like time complexity, space complexity is expressed in Big O notation. It takes into account the memory required for variables, data structures, and function calls.
For example:
- O(1) space complexity means that the algorithm uses a constant amount of memory, regardless of the input size.
- O(n) space complexity means that the memory usage grows linearly with the size of the input.
What is the Difference Between Best Case, Average Case, and Worst Case in Big O Notation?
When analyzing an algorithm, we often consider three different scenarios:
- Best Case: The scenario where the algorithm performs the fewest possible steps.
- Example: For linear search, the best case is when the element to be found is the first element, yielding O(1) time complexity.
- Average Case: The scenario that represents the typical or expected behavior of the algorithm. It’s often more difficult to calculate but provides a more realistic performance measure.
- Example: In binary search, the average case is typically O(log n).
- Worst Case: The scenario where the algorithm performs the maximum number of steps. Big O notation is primarily concerned with this case, as it provides the upper bound on time complexity.
- Example: In bubble sort, the worst-case scenario is when the array is in reverse order, yielding O(n²) time complexity.
How Do You Determine the Big O Notation of an Algorithm?
To determine the Big O notation of an algorithm, follow these steps:
- Identify the Basic Operations: Look at the basic steps the algorithm performs, such as comparisons, assignments, or iterations.
- Count the Number of Operations: Analyze how the number of operations grows with respect to the input size n.
- Identify the Dominant Term: Focus on the term that grows the fastest as n increases. For example, if the total number of operations is 3n³ + 2n² + 5n + 10, the dominant term is n³, and the algorithm’s complexity is O(n³).
- Ignore Constants: In Big O notation, constants, and lower-order terms are ignored because they don’t significantly affect the growth rate for large n. Therefore, O(3n) = O(n) and O(2n² + n) = O(n²).
What is the Difference Between O(n) and O(n²)?
O(n), or linear time complexity, means that the algorithm’s running time grows in direct proportion to the input size. If the input doubles, the running time also doubles.
O(n²), or quadratic time complexity, means that the algorithm’s running time grows quadratically with the input size. If the input size doubles, the running time increases fourfold.
For example:
- O(n): Traversing an array to find a specific element requires checking each element, making the time complexity linear.
- O(n²): In bubble sort, each element is compared to every other element, resulting in quadratic time complexity.
What is Logarithmic Time Complexity (O(log n))?
Logarithmic time complexity denoted as O(log n), occurs when an algorithm reduces the problem size by a constant factor at each step. Algorithms with logarithmic time complexity are highly efficient for large inputs because they reduce the input size exponentially.
Example: Binary search is a classic example of an O(log n) algorithm. It works by repeatedly dividing the search space in half, significantly reducing the number of comparisons required.
int binarySearch(int arr[], int l, int r, int x) {
while (l <= r) {
int mid = l + (r - l) / 2;
if (arr[mid] == x)
return mid;
if (arr[mid] < x)
l = mid + 1;
else
r = mid - 1;
}
return -1;
}In this example, the array is divided into two halves at each step, leading to O(log n) complexity.
What is Quadratic Time Complexity (O(n²))?
Quadratic time complexity denoted as O(n²), occurs when the running time of an algorithm grows proportionally to the square of the input size. This is common in algorithms that involve nested loops, where each element is compared or processed in relation to every other element.
Example: Bubble sort has O(n²) complexity because each element is compared to every other element.
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
}
}
}
}In this case, the algorithm runs n times for each of the n elements, resulting in O(n²) complexity.
What is Exponential Time Complexity (O(2ⁿ))?
Exponential time complexity denoted as O(2ⁿ), means that the running time doubles with each additional input element. This type of complexity is often seen in recursive algorithms that solve problems by dividing them into smaller subproblems.
Example: Generating all subsets of a set is an example of an O(2ⁿ) algorithm.
void generateSubsets(int arr[], int n) {
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
if (i & (1 << j)) {
cout << arr[j] << " ";
}
}
cout << endl;
}
}In this case, for a set of size n, there are 2ⁿ possible subsets, resulting in exponential time complexity.
How Do Recursive Algorithms Affect Time Complexity?
Recursive algorithms often have higher time complexity due to the repeated function calls and the way problems are broken down. To analyze a recursive algorithm’s time complexity, we use a recurrence relation, which describes how the function depends on smaller instances of the same problem.
For example, in binary search (a recursive algorithm), the recurrence relation is T(n) = T(n/2) + O(1), which resolves to O(log n).
However, in more complex recursive algorithms like the Tower of Hanoi problem, the time complexity is O(2ⁿ) due to the exponential number of recursive calls required to move all disks from one peg to another.
Can Big O Notation Be Applied to Space Complexity?
Yes, Big O notation is also used to describe the space complexity of an algorithm, which refers to the amount of memory required relative to the input size. The steps to calculate space complexity are similar to time complexity:
- Determine the Variables: Identify the amount of memory used for variables, data structures, and recursion stacks.
- Ignore Constants: Focus on how memory usage grows as n increases.
- Focus on the Dominant Term: Identify the term with the highest growth rate.
For example:
- An algorithm with O(1) space complexity uses a constant amount of memory regardless of input size.
- An algorithm with O(n) space complexity uses memory that grows linearly with the input size, such as storing an array of n elements.
What is the Difference Between Time Complexity and Space Complexity?
Time complexity refers to how the running time of an algorithm increases as the input size grows, while space complexity refers to how much memory an algorithm requires. Both are important when evaluating an algorithm’s overall efficiency.
- Time complexity focuses on the number of operations required to complete a task.
- Space complexity focuses on the amount of memory needed to store data during execution.
For example:
- Merge sort has a time complexity of O(n log n) but a space complexity of O(n) because it requires additional memory to store temporary arrays.
How Does Big O Notation Help in Real-World Applications?
In real-world applications, Big O notation helps developers design algorithms that scale efficiently as data grows. This is particularly important in fields like:
- Web Development: Efficient algorithms ensure that websites and applications load quickly, even with a large number of users.
- Data Science: Algorithms that handle massive datasets need to be optimized for both time and space to ensure fast processing.
- Mobile Applications: Limited resources on mobile devices mean that algorithms must be both time- and space-efficient.
- Machine Learning: Training models on large datasets requires algorithms that can handle high computational complexity efficiently.
By understanding Big O notation, developers can predict an algorithm’s performance and ensure that systems remain responsive and efficient, even as they grow.
