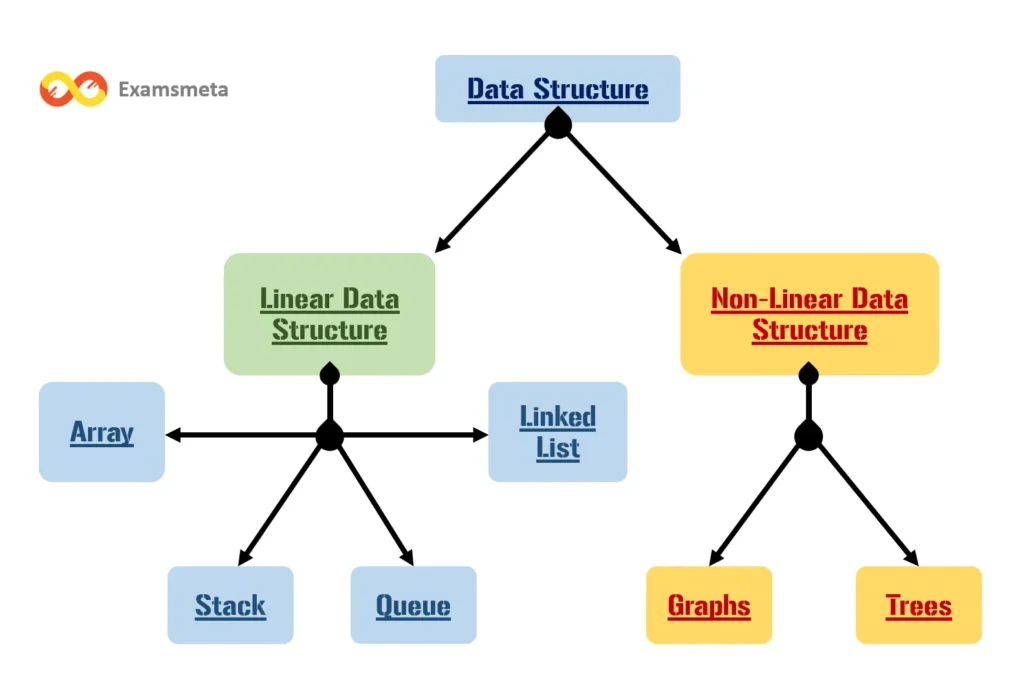
When we dive into the world of computer science, understanding the structure and organization of data becomes essential for building efficient algorithms. The way data is stored, retrieved, and managed directly affects the performance of software applications. Two fundamental categories that classify data structures are linear data structures and non-linear data structures. These two types differ not just in their organizational structure but also in the way we access, traverse, and manipulate the data. In this detailed post, we will explore both linear and non-linear data structures, highlighting their characteristics, differences, and applications in various real-life scenarios.
Table of Contents
- Also Read: Understanding Data Structures: An In-Depth Exploration
- Also Read: A Comprehensive Guide to DSA: Data Structures and Algorithms
Linear Data Structures
A linear data structure is one in which the elements are arranged in a sequential manner. In other words, the elements are organized one after the other, forming a straight line. The key characteristic of linear structures is that there is a single path to traverse the data. Because of their simple structure, linear data structures are easy to implement and manage, and we can access the elements in a single run, i.e., they provide sequential access.
Some common examples of linear data structures include:
- Arrays
- Stacks
- Queues
- Linked Lists
1. Array
An array is the most basic type of data structure in computer science. It stores elements of the same data type in contiguous memory locations. Arrays allow easy access to data using indices, which act as pointers to specific memory locations.
For instance, consider a scenario where we need to store the prices of ten different cars. Instead of creating ten separate variables, we can simply create an array that holds all the prices together in a structured format. Each element in the array can be accessed by its index, starting from index 0 for the first element.
Example:
int carPrices[10] = {20000, 25000, 18000, 30000, 40000, 15000, 22000, 33000, 29000, 50000};This is far more efficient than creating ten separate variables, saving both time and memory. Arrays are particularly useful in situations where we need random access to data, as any element can be accessed directly using its index.
However, arrays come with certain limitations:
- Fixed Size: Once declared, the size of an array cannot be changed, meaning it can’t dynamically adjust its capacity.
- Homogeneous Elements: All elements in an array must be of the same data type (e.g., all integers, all floats, etc.).
2. Stack
A stack is a linear data structure that follows the principle of Last In, First Out (LIFO). This means that the last element added to the stack is the first one to be removed. We can imagine a stack like a pile of books, where you can only add or remove the topmost book.
Stacks have two main operations:
- Push: Adds an element to the top of the stack.
- Pop: Removes the element from the top of the stack.
A real-world example of a stack can be seen in the undo function of text editors. Each change we make is “pushed” onto the stack, and when we press the undo button, the most recent change is “popped” off the stack.
Example in Programming:
stack.push(10);
stack.push(20);
stack.pop(); // Removes 20, as it was the last element addedStacks are widely used in scenarios where reversibility is important, such as recursion, expression evaluation, and syntax parsing.
3. Queue
A queue is similar to a stack, but it follows the principle of First In, First Out (FIFO). This means that the first element added to the queue is the first one to be removed. A queue operates much like a line of people waiting for their turn—those who arrive first get served first.
There are two primary operations in a queue:
- Enqueue: Adds an element to the rear (end) of the queue.
- Dequeue: Removes an element from the front (start) of the queue.
Queues are commonly used in scheduling systems and task management. For instance, consider the case of printer queues, where documents are printed in the order they are submitted.
Example:
queue.enqueue(10);
queue.enqueue(20);
queue.dequeue(); // Removes 10, as it was the first element addedThere are various types of queues, such as circular queues, priority queues, and double-ended queues (Deque), each designed for specific types of processing.
4. Linked List
A linked list is a collection of nodes, where each node contains a data element and a pointer (or reference) to the next node in the sequence. Unlike arrays, linked lists are dynamic in size, meaning they can grow and shrink as needed during the execution of a program.
There are several types of linked lists, including:
- Singly Linked List: Each node points to the next node.
- Doubly Linked List: Each node points to both the next and previous nodes.
- Circular Linked List: The last node points back to the first node, forming a circular structure.
Linked lists are useful when frequent insertions and deletions are required, as these operations can be performed without shifting elements, unlike arrays.
Example of a Singly Linked List in C:
struct Node {
int data;
struct Node* next;
};Linked lists are particularly useful in situations where the data set may change in size dynamically, such as in memory management or graph implementations.
5. Hash Tables
Hash tables can be implemented as both linear and non-linear data structures, depending on the design. In a hash table, data is stored in key-value pairs. Each key is processed through a hash function that computes a unique index (or hash) to determine where the value will be stored in memory.
Hash tables are extremely useful for applications requiring fast lookups, such as dictionaries, databases, and caches. They offer an average time complexity of O(1) for search, insert, and delete operations.
Non-Linear Data Structures
Unlike linear data structures, non-linear data structures organize data in a hierarchical or interconnected manner. Here, the elements are not arranged sequentially, and they can have complex relationships with one another. Non-linear structures allow for more efficient memory utilization in some cases and are particularly useful in applications where the data needs to be represented in a tree-like or network-like structure.
The two most common non-linear data structures are:
- Trees
- Graphs
1. Trees
A tree is a hierarchical data structure that consists of nodes, with one node designated as the root and the remaining nodes forming branches. Each node in a tree has zero or more children, and a node with no children is called a leaf.
The parent-child relationship in trees is central to their structure, and trees are often used to represent hierarchical data, such as file systems, organizational charts, or decision trees.
Key Types of Trees:
- Binary Tree: Each node has at most two children (left and right).
- Binary Search Tree (BST): A type of binary tree where the left child contains values smaller than the parent, and the right child contains values larger than the parent.
- AVL Tree: A self-balancing binary search tree where the difference in heights of the left and right subtrees is at most one for all nodes.
Example of Tree Application:
Consider the hierarchical structure of a company, where the CEO is the root node, the department heads are the children, and the employees under each department are the leaf nodes.
Trees are essential in tasks like parsing expressions in compilers, organizing XML/HTML documents, and implementing Trie structures for fast dictionary lookups.
2. Graphs
A graph is a collection of vertices (or nodes) and edges that connect pairs of vertices. Unlike trees, graphs are more flexible and can represent any kind of relationship between nodes, including cyclic relationships.
Graphs are of two types:
- Directed Graph (Digraph): The edges have a direction, indicating a one-way relationship between nodes.
- Undirected Graph: The edges do not have a direction, representing a two-way relationship.
Graphs are used extensively in real-life applications, such as representing social networks, transportation networks, telecommunication networks, and even in AI for search algorithms.
For instance, the representation of a friendship network in a social media platform can be modeled using an undirected graph, where each vertex represents a user, and the edges represent friendships.
Graphs also form the backbone of numerous algorithms, such as:
- Dijkstra’s Algorithm for shortest path calculation.
- Kruskal’s Algorithm for minimum spanning trees.
- Depth First Search (DFS) and Breadth First Search (BFS) for exploring graphs.
Key Differences Between Linear and Non-Linear Data Structures
| Criteria | Linear Data Structure | Non-Linear Data Structure |
|---|---|---|
| Definition | A data structure where elements are arranged sequentially, one after the other. | A data structure where elements are arranged hierarchically or non-sequentially. |
| Traversal | All elements can be traversed in a single run, sequentially. | All elements cannot be traversed in a single run. Multiple paths may exist. |
| Memory Utilization | Inefficient memory utilization as elements are stored contiguously. | Efficient memory utilization as elements can be stored non-contiguously. |
| Ease of Implementation | Easier to implement due to the sequential arrangement of elements. | More complex to implement due to hierarchical or interconnected relationships. |
| Flexibility | Less flexible; fixed size in structures like arrays. | More flexible; dynamic size in structures like trees and graphs. |
| Examples | Arrays, Stacks, Queues, Linked Lists. | Trees (Binary Tree, AVL Tree), Graphs. |
| Insertion and Deletion | Operations are relatively straightforward but can be time-consuming (e.g., in arrays). | Operations are more complex but can be more efficient depending on the structure (e.g., in trees). |
| Element Access | Elements can be accessed in linear order, with direct access possible in arrays. | Accessing elements is more complex and depends on the structure (e.g., in trees or graphs). |
| Time Complexity (Search) | Searching for an element in a linear data structure may take O(n) time. | Searching can be more efficient, such as O(log n) in balanced trees like BST. |
| Connections between Elements | Each element is connected to its previous and next element. | Each element may be connected to multiple other elements in a hierarchical or network manner. |
| Level of Structure | Elements are organized on a single level. | Elements are organized at multiple levels, often hierarchical. |
| Use of Memory | Memory is allocated in a contiguous block (in arrays, for example). | Memory is allocated dynamically (in linked lists, trees, and graphs). |
| Complexity | Less complex to handle and use, especially for smaller datasets. | More complex, especially for larger datasets or where relationships between elements matter. |
| Data Relationships | Data elements have a linear relationship (one-to-one). | Data elements have hierarchical or network relationships (one-to-many or many-to-many). |
| Real-World Examples | Array: An ordered list of items like daily expenses. Queue: People lining up to buy movie tickets. | Tree: Hierarchical organization like a family tree or file directory. Graph: Social networks or maps where locations are interconnected. |
| Operations | Easier and faster for tasks like accessing elements sequentially. | More efficient for complex tasks like hierarchical or network-related data operations. |
| Representation | Can be visualized as a straight line or list. | Can be visualized as a tree or network with branching paths. |
| Suitability for Algorithms | Useful in simple algorithms like searching and sorting (e.g., Bubble Sort, Linear Search). | Crucial for complex algorithms like graph traversal (DFS, BFS) and tree-based sorting. |
| Data Access Method | Sequential access, where elements are accessed one by one. | Can be accessed in a more non-linear manner, allowing for hierarchical traversal. |
| Usage Scenarios | Preferred when the order of elements is crucial or for simple data management. | Best suited for complex problems where relationships between elements need to be modeled (e.g., networks, hierarchies). |
Examples in Python, C++, and JavaScript demonstrate the differences between Linear & Non-Linear Data Structures.
Example 1: Linear Data Structure – Array
Python Example:
# Example of a Linear Data Structure: Array
# Python List used as an array
# Define an array
cars = ["Toyota", "Honda", "Ford", "Tesla", "BMW"]
# Accessing elements by index
print("Accessing elements in array:")
print(cars[0]) # First element
print(cars[2]) # Third element
print(cars[-1]) # Last element
# Inserting an element
cars.append("Mercedes")
print("\nArray after appending:")
print(cars)
# Removing an element
cars.remove("Ford")
print("\nArray after removing 'Ford':")
print(cars)Output:
Accessing elements in array:
Toyota
Ford
BMW
Array after appending:
['Toyota', 'Honda', 'Ford', 'Tesla', 'BMW', 'Mercedes']
Array after removing 'Ford':
['Toyota', 'Honda', 'Tesla', 'BMW', 'Mercedes']C++ Example:
#include <iostream>
#include <vector>
using namespace std;
int main() {
// Example of a Linear Data Structure: Array
// Using C++ vector to represent an array
vector<string> cars = {"Toyota", "Honda", "Ford", "Tesla", "BMW"};
// Accessing elements by index
cout << "Accessing elements in array:" << endl;
cout << cars[0] << endl; // First element
cout << cars[2] << endl; // Third element
cout << cars[cars.size() - 1] << endl; // Last element
// Inserting an element
cars.push_back("Mercedes");
cout << "\nArray after appending:" << endl;
for (string car : cars) {
cout << car << " ";
}
cout << endl;
// Removing an element
cars.erase(cars.begin() + 2); // Remove "Ford"
cout << "\nArray after removing 'Ford':" << endl;
for (string car : cars) {
cout << car << " ";
}
cout << endl;
return 0;
}Output:
Accessing elements in array:
Toyota
Ford
BMW
Array after appending:
Toyota Honda Ford Tesla BMW Mercedes
Array after removing 'Ford':
Toyota Honda Tesla BMW Mercedes JavaScript Example:
// Example of a Linear Data Structure: Array
// Define an array
let cars = ["Toyota", "Honda", "Ford", "Tesla", "BMW"];
// Accessing elements by index
console.log("Accessing elements in array:");
console.log(cars[0]); // First element
console.log(cars[2]); // Third element
console.log(cars[cars.length - 1]); // Last element
// Inserting an element
cars.push("Mercedes");
console.log("\nArray after appending:");
console.log(cars);
// Removing an element
cars.splice(cars.indexOf("Ford"), 1); // Remove "Ford"
console.log("\nArray after removing 'Ford':");
console.log(cars);Output:
Accessing elements in array:
Toyota
Ford
BMW
Array after appending:
[ 'Toyota', 'Honda', 'Ford', 'Tesla', 'BMW', 'Mercedes' ]
Array after removing 'Ford':
[ 'Toyota', 'Honda', 'Tesla', 'BMW', 'Mercedes' ]Example 2: Non-Linear Data Structure – Binary Tree
Python Example:
# Example of a Non-Linear Data Structure: Binary Tree
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert function to add a node in the binary tree
def insert(root, key):
if root is None:
return Node(key)
else:
if key < root.data:
root.left = insert(root.left, key)
else:
root.right = insert(root.right, key)
return root
# Inorder traversal (left-root-right)
def inorder(root):
if root:
inorder(root.left)
print(root.data, end=" ")
inorder(root.right)
# Creating binary tree and inserting nodes
root = Node(50)
insert(root, 30)
insert(root, 70)
insert(root, 20)
insert(root, 40)
insert(root, 60)
insert(root, 80)
print("Inorder traversal of the binary tree:")
inorder(root)Output:
Inorder traversal of the binary tree:
20 30 40 50 60 70 80 C++ Example:
#include <iostream>
using namespace std;
// Binary Tree Node structure
class Node {
public:
int data;
Node* left;
Node* right;
Node(int value) {
data = value;
left = right = NULL;
}
};
// Function to insert a new node
Node* insert(Node* root, int key) {
if (root == NULL) {
return new Node(key);
}
if (key < root->data) {
root->left = insert(root->left, key);
} else {
root->right = insert(root->right, key);
}
return root;
}
// Inorder Traversal
void inorder(Node* root) {
if (root != NULL) {
inorder(root->left);
cout << root->data << " ";
inorder(root->right);
}
}
int main() {
Node* root = new Node(50);
insert(root, 30);
insert(root, 70);
insert(root, 20);
insert(root, 40);
insert(root, 60);
insert(root, 80);
cout << "Inorder traversal of the binary tree:" << endl;
inorder(root);
return 0;
}Output:
Inorder traversal of the binary tree:
20 30 40 50 60 70 80 JavaScript Example:
// Example of a Non-Linear Data Structure: Binary Tree
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
// Insert function to add a node in the binary tree
function insert(root, key) {
if (root === null) {
return new Node(key);
}
if (key < root.data) {
root.left = insert(root.left, key);
} else {
root.right = insert(root.right, key);
}
return root;
}
// Inorder traversal (left-root-right)
function inorder(root) {
if (root !== null) {
inorder(root.left);
console.log(root.data + " ");
inorder(root.right);
}
}
// Creating binary tree and inserting nodes
let root = new Node(50);
insert(root, 30);
insert(root, 70);
insert(root, 20);
insert(root, 40);
insert(root, 60);
insert(root, 80);
console.log("Inorder traversal of the binary tree:");
inorder(root);Output:
Inorder traversal of the binary tree:
20
30
40
50
60
70
80 Conclusion
Understanding the differences between linear and non-linear data structures is critical for selecting the right structure for a given problem. While linear structures are easier to implement and perfect for situations that require simple sequential access, non-linear structures are more powerful when dealing with complex relationships or hierarchical data. Each type of structure offers unique advantages and plays a pivotal role in computer science and software development.
By mastering both linear and non-linear data structures, you’ll be well-equipped to handle a wide range of programming challenges, from organizing simple lists of data to building sophisticated algorithms that can solve complex, real-world problems.
Related Articles
- Understanding Big-Theta (Θ) Notation in Algorithm Analysis
- Big-Omega (Ω) Notation in Algorithm Analysis: A Comprehensive Guide
- Big O Notation Tutorial – A Comprehensive Guide to Algorithm Complexity Analysis
- Asymptotic Notation and Complexity Analysis of Algorithms
- Understanding Algorithms in Computer Science: A Comprehensive Guide
- Understanding Trie Data Structure in Depth: A Comprehensive Guide
- Real-Life Example of the Brute Force Algorithm: Password Cracking
- Brute Force Algorithm: Comprehensive Exploration, Pros, Cons, & Applications
- Analyzing an Algorithm and its Complexity: A Comprehensive Guide
- Understanding Algorithms: A Comprehensive Introduction
- Understanding Hashing: The Key to Fast and Efficient Data Storage and Retrieval
- Hierarchical Data Structures: Binary Trees, Binary Search Trees, Heaps, & Hashing
- Comprehensive Overview on Applications of Arrays, Advantages & Disadvantages of Arrays
- Matrix Data Structure: A Comprehensive Guide to the Two-Dimensional Array
- Introduction to Array Data Structures: A Comprehensive Guide
- Understanding Linear Data Structures: A Comprehensive Exploration
- Difference Between Linear & Non-Linear Data Structures: A Comprehensive Overview
- Tree Data Structures: Definitions, Types, Applications, & Comprehensive Exploration
- Cyclic Graphs: Structure, Applications, Advantages, & Challenges in Data Structures
- Introduction to Directed Acyclic Graph (DAG): A Comprehensive Exploration with Examples
- Strongly, Unilaterally, and Weakly Connected Graphs in Data Structures
- Unweighted Graphs: Definition, Applications, Advantages, and Disadvantages
- Comprehensive Guide to Adjacency Lists in Data Structures
- Adjacency Matrix: A Comprehensive Guide to Graph Representation
- Understanding Weighted Graphs: A Comprehensive Exploration
- Understanding Undirected Graphs: Structure, Applications, and Advantages
- Understanding Directed Graphs: Characteristics, Applications, & Real-World Examples
- Graph Data Structure in Computer Science: A Comprehensive Exploration
- Understanding Data Structures: An In-Depth Exploration
- A Comprehensive Guide to DSA: Data Structures and Algorithms
Read More Articles
- Data Structure (DS) Array:
- Why the Analysis of Algorithms is Important?
- Worst, Average, and Best Case Analysis of Algorithms: A Comprehensive Guide
- Understanding Pointers in C Programming: A Comprehensive Guide
- Understanding Arrays in Data Structures: A Comprehensive Exploration
- Memory Allocation of an Array: An In-Depth Comprehensive Exploration
- Understanding Basic Operations in Arrays: A Comprehensive Guide
- Understanding 2D Arrays in Programming: A Comprehensive Guide
- Mapping a 2D Array to a 1D Array: A Comprehensive Exploration
- Data Structure Linked List:
- Understanding Linked Lists in Data Structures: A Comprehensive Exploration
- Types of Linked List: Detailed Exploration, Representations, and Implementations
- Understanding Singly Linked Lists: A Detailed Exploration
- Understanding Doubly Linked List: A Comprehensive Guide
- Operations of Doubly Linked List with Implementation: A Detailed Exploration
- Insertion in Doubly Linked List with Implementation: A Detailed Exploration
- Inserting a Node at the beginning of a Doubly Linked List: A Detailed Exploration
- Inserting a Node After a Given Node in a Doubly Linked List: A Detailed Exploration
- Inserting a Node Before a Given Node in a Doubly Linked List: A Detailed Exploration
- Inserting a Node at a Specific Position in a Doubly Linked List: A Detailed Exploration
- Inserting a New Node at the End of a Doubly Linked List: A Detailed Exploration
- Deletion in a Doubly Linked List with Implementation: A Comprehensive Guide
- Deletion at the Beginning in a Doubly Linked List: A Detailed Exploration
- Deletion after a given node in Doubly Linked List: A Comprehensive Guide
- Deleting a Node Before a Given Node in a Doubly Linked List: A Detailed Exploration
- Deletion at a Specific Position in a Doubly Linked List: A Detailed Exploration
- Deletion at the End in Doubly Linked List: A Comprehensive Exploration
- Introduction to Circular Linked Lists: A Comprehensive Guide
- Understanding Circular Singly Linked Lists: A Comprehensive Guide
- Circular Doubly Linked List: A Comprehensive Guide
- Insertion in Circular Singly Linked List: A Comprehensive Guide
- Insertion in an Empty Circular Linked List: A Detailed Exploration
- Insertion at the Beginning in Circular Linked List: A Detailed Exploration
- Insertion at the End of a Circular Linked List: A Comprehensive Guide
- Insertion at a Specific Position in a Circular Linked List: A Detailed Exploration
- Deletion from a Circular Linked List: A Comprehensive Guide
- Deletion from the Beginning of a Circular Linked List: A Detailed Exploration
- Deletion at Specific Position in Circular Linked List: A Detailed Exploration
- Deletion at the End of a Circular Linked List: A Comprehensive Guide
- Searching in a Circular Linked List: A Comprehensive Exploration
Frequently Asked Questions (FAQs) on Data Structures
What is a Data Structure?
A data structure is a specialized way of organizing and storing data in a computer so that it can be used efficiently. Different data structures are suited for different kinds of applications, and they determine the way data can be accessed, manipulated, and stored. Common examples of data structures include arrays, linked lists, stacks, queues, trees, and graphs. Choosing the right data structure impacts the performance and complexity of algorithms, allowing for optimized operations such as searching, sorting, and inserting.
What are the main types of Data Structures?
Data structures can be broadly categorized into two main types:
- Linear Data Structures: In these structures, data elements are arranged sequentially or linearly, where each element is attached to its previous and next adjacent elements. Examples include arrays, stacks, queues, and linked lists.
- Non-linear Data Structures: In these structures, data elements are not organized in a linear manner. Instead, they may be arranged hierarchically or with complex relationships between elements. Examples include trees and graphs.
What is the difference between Linear and Non-Linear Data Structures?
- Linear Data Structures: The elements are arranged sequentially, one after the other. Examples include arrays, stacks, and queues. Linear structures are easier to implement but may not be the most memory-efficient for complex relationships.
- Non-Linear Data Structures: The elements are arranged hierarchically or connected with multiple relationships. Examples include trees and graphs. These structures are more complex but offer more efficient memory utilization for hierarchical or interconnected data.
What is an Array in Data Structures?
An array is a collection of elements, all of the same type, stored in contiguous memory locations. The size of an array is fixed, and elements are accessed using indices, which start from zero. Arrays provide fast access to elements because any element can be accessed directly by its index in O(1) time. However, their fixed size makes arrays less flexible than other data structures like linked lists.
What is a Stack?
A stack is a linear data structure that follows the LIFO (Last In, First Out) principle. This means that the last element added to the stack is the first one to be removed. Stacks are used in many areas of computer science, including function call management, expression evaluation, and backtracking algorithms. Operations on a stack include:
- Push: Add an element to the top of the stack.
- Pop: Remove an element from the top of the stack.
What is a Queue?
A queue is a linear data structure that follows the FIFO (First In, First Out) principle, meaning that the first element added to the queue will be the first one to be removed. Queues are widely used in systems that require sequential processing, such as task scheduling, printer management, and customer service systems. Operations on a queue include:
- Enqueue: Add an element to the rear of the queue.
- Dequeue: Remove an element from the front of the queue.
What is a Linked List?
A linked list is a linear data structure where elements, called nodes, are stored in non-contiguous memory locations. Each node contains two parts: data and a pointer (or reference) to the next node in the sequence. Linked lists are dynamic in size, meaning they can grow and shrink during runtime, unlike arrays. Types of linked lists include:
- Singly Linked List: Each node points to the next node.
- Doubly Linked List: Each node points to both the next and previous nodes.
- Circular Linked List: The last node points back to the first node.
What is a Tree in Data Structures?
A tree is a hierarchical data structure consisting of nodes connected by edges. Each node contains a value, and the nodes are connected in a parent-child relationship. The root is the topmost node, and the leaves are nodes with no children. Common types of trees include:
- Binary Tree: Each node has at most two children.
- Binary Search Tree (BST): A binary tree where the left child contains values smaller than the parent and the right child contains values larger than the parent.
- AVL Tree: A self-balancing binary search tree where the heights of the left and right subtrees differ by at most one.
What is a Graph in Data Structures?
A graph is a non-linear data structure consisting of vertices (nodes) and edges (connections between nodes). Graphs can be directed (with one-way relationships) or undirected (with two-way relationships). Graphs are commonly used to represent networks, such as social networks, communication systems, and transportation systems. Algorithms like Dijkstra’s and Kruskal’s use graphs to solve problems related to shortest paths and minimum-spanning trees.
What are the applications of Stacks?
Stacks have a wide range of applications, including:
- Expression Evaluation: Stacks are used to evaluate infix, prefix, and postfix expressions.
- Function Call Management: The system call stack is used to manage function calls in programming, keeping track of function parameters, return values, and local variables.
- Backtracking Algorithms: Algorithms like DFS (Depth First Search) in graph traversal use stacks to store and retrieve the nodes to be visited.
What are the applications of Queues?
Queues are used in various real-world and computational scenarios, such as:
- CPU Scheduling: Operating systems use queues to manage processes in round-robin scheduling.
- Task Management: Queues are used in task scheduling systems where tasks need to be executed in the order they are received.
- Breadth-First Search (BFS): In graph traversal, BFS uses a queue to explore nodes level by level.
What is the difference between a Singly Linked List and a Doubly Linked List?
A Singly Linked List is a type of linked list where each node has a reference to the next node, allowing traversal in only one direction. In contrast, a Doubly Linked List allows traversal in both directions because each node has references to both the next and the previous nodes. While Singly Linked Lists are more memory-efficient, Doubly Linked Lists provide more flexibility in traversal and deletion operations.
What is a Binary Search Tree (BST)?
A Binary Search Tree (BST) is a special type of binary tree where every node follows the property that:
- The left child of a node contains a value less than the node’s value.
- The right child of a node contains a value greater than the node’s value.
This property makes BSTs useful for searching, inserting, and deleting elements efficiently. The average time complexity for these operations is O(log n) when the tree is balanced.
What are the main operations on Trees?
Operations on trees include:
- Insertion: Adding a new node to the tree while maintaining the tree’s structure.
- Deletion: Removing a node from the tree while ensuring the structure remains valid.
- Traversal: Visiting each node in the tree in a specific order. There are three main traversal methods:
- In-order Traversal: Visits the left subtree, the root, and then the right subtree.
- Pre-order Traversal: Visits the root, the left subtree, and then the right subtree.
- Post-order Traversal: Visits the left subtree, the right subtree, and then the root.
What is a Hash Table?
A hash table is a data structure that stores data in an array-like format, where each data element is assigned a unique index generated by a hash function. Hash tables are particularly useful for efficient lookup, insertion, and deletion operations, with an average time complexity of O(1). They are widely used in applications such as dictionaries, database indexing, and caches.
What is a Priority Queue?
A priority queue is a type of queue where each element is associated with a priority. In a regular queue, elements are dequeued in the order they were enqueued (FIFO). However, in a priority queue, elements with higher priorities are dequeued before elements with lower priorities. This structure is often implemented using heaps and is used in algorithms like Dijkstra’s shortest path algorithm.
What is a Circular Queue?
A circular queue is a linear data structure that connects the last position of the queue back to the first position, forming a circle. It overcomes the limitation of the regular queue, where the rear pointer would reach the end, leaving no space for further insertions. Circular queues are useful in applications such as buffer management, where data needs to be processed in a loop.
What is Depth First Search (DFS) in Graphs?
Depth First Search (DFS) is an algorithm for traversing or searching through a graph. It starts at the root (or an arbitrary node) and explores as far as possible along each branch before backtracking. DFS uses a stack data structure (often implemented via recursion) and is useful in situations like detecting cycles in graphs and solving maze problems.
What is Breadth First Search (BFS) in Graphs?
Breadth First Search (BFS) is another graph traversal algorithm, which explores all neighbors of a node before moving on to the next level of nodes. It uses a queue data structure and is ideal for finding the shortest path in unweighted graphs and for applications like peer-to-peer networks and web crawlers.
What are some common real-world applications of Trees and Graphs?
- Trees:
- Binary Search Trees are used in databases to store records and allow fast retrieval of data.
- Trie Trees are used for autocomplete functionality and dictionary applications.
- Heap Trees are used in priority queues, scheduling algorithms, and memory management.
- Graphs:
- Social networks use graphs to represent relationships between users.
- GPS and mapping systems use graphs to represent routes and find the shortest path between two locations.
- Telecommunication networks use graphs to model connections between switches and routers.
By understanding these data structures and their use cases, developers can craft efficient algorithms tailored to specific problems, ultimately enhancing application performance and scalability.
